Menu Close

I-0-1-lnt-1-t-2-dt-Helpe-me-please-

Tinku Tara 0 Comments
Pin




Question Number 120383 by SOMEDAVONG last updated on 31/Oct/20
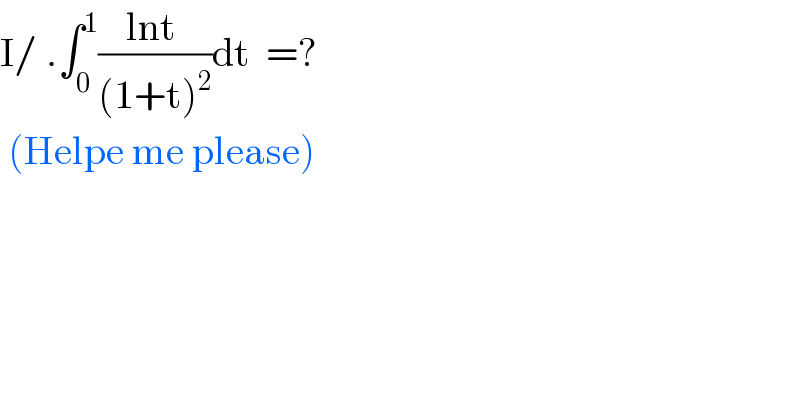
I/ .∫_0 ^1 ((lnt )/((1+t)^2 ))dt =? (Helpe me please)
$$\mathrm{I}/\:.\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lnt}\:}{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt}\:\:=? \\ $$$$\:\left(\mathrm{Helpe}\:\mathrm{me}\:\mathrm{please}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 31/Oct/20
∫_0 ^1 ((logt)/((1+t)^2 ))dt =−[((logt)/(t+1))]_0 ^1 +∫_0 ^1 (1/(t(t+1)))dt =[log((t/(t+1)))]_0 ^1 =−log(2)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=−\left[\frac{{logt}}{{t}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{t}\left({t}+\mathrm{1}\right)}{dt} \\ $$$$=\left[{log}\left(\frac{{t}}{{t}+\mathrm{1}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =−{log}\left(\mathrm{2}\right) \\ $$
Commented by SOMEDAVONG last updated on 31/Oct/20
(Thank you so much)
$$\left(\boldsymbol{\mathrm{Thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{much}}\right) \\ $$
Answered by Olaf last updated on 31/Oct/20
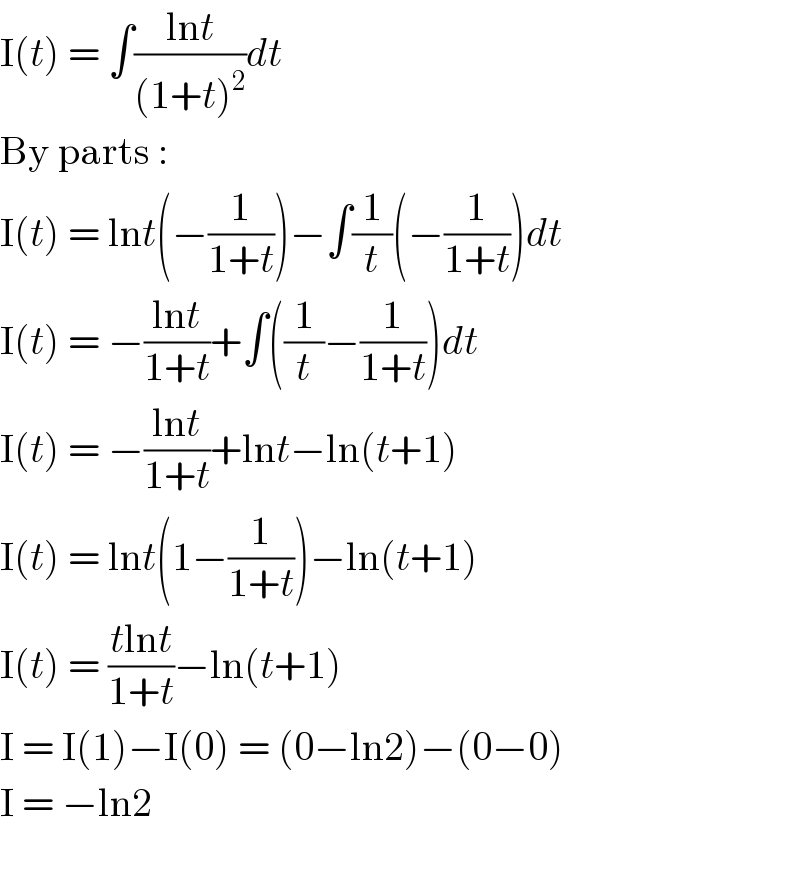
I(t) = ∫((lnt)/((1+t)^2 ))dt By parts : I(t) = lnt(−(1/(1+t)))−∫(1/t)(−(1/(1+t)))dt I(t) = −((lnt)/(1+t))+∫((1/t)−(1/(1+t)))dt I(t) = −((lnt)/(1+t))+lnt−ln(t+1) I(t) = lnt(1−(1/(1+t)))−ln(t+1) I(t) = ((tlnt)/(1+t))−ln(t+1) I = I(1)−I(0) = (0−ln2)−(0−0) I = −ln2
$$\mathrm{I}\left({t}\right)\:=\:\int\frac{\mathrm{ln}{t}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$$\mathrm{By}\:\mathrm{parts}\:: \\ $$$$\mathrm{I}\left({t}\right)\:=\:\mathrm{ln}{t}\left(−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)−\int\frac{\mathrm{1}}{{t}}\left(−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$\mathrm{I}\left({t}\right)\:=\:−\frac{\mathrm{ln}{t}}{\mathrm{1}+{t}}+\int\left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right){dt} \\ $$$$\mathrm{I}\left({t}\right)\:=\:−\frac{\mathrm{ln}{t}}{\mathrm{1}+{t}}+\mathrm{ln}{t}−\mathrm{ln}\left({t}+\mathrm{1}\right) \\ $$$$\mathrm{I}\left({t}\right)\:=\:\mathrm{ln}{t}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)−\mathrm{ln}\left({t}+\mathrm{1}\right) \\ $$$$\mathrm{I}\left({t}\right)\:=\:\frac{{t}\mathrm{ln}{t}}{\mathrm{1}+{t}}−\mathrm{ln}\left({t}+\mathrm{1}\right) \\ $$$$\mathrm{I}\:=\:\mathrm{I}\left(\mathrm{1}\right)−\mathrm{I}\left(\mathrm{0}\right)\:=\:\left(\mathrm{0}−\mathrm{ln2}\right)−\left(\mathrm{0}−\mathrm{0}\right) \\ $$$$\mathrm{I}\:=\:−\mathrm{ln2} \\ $$$$ \\ $$
Commented by SOMEDAVONG last updated on 31/Oct/20
(Thank you so much sir)
$$\left(\boldsymbol{\mathrm{Thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{much}}\:\boldsymbol{\mathrm{sir}}\right) \\ $$
Answered by Lordose last updated on 31/Oct/20
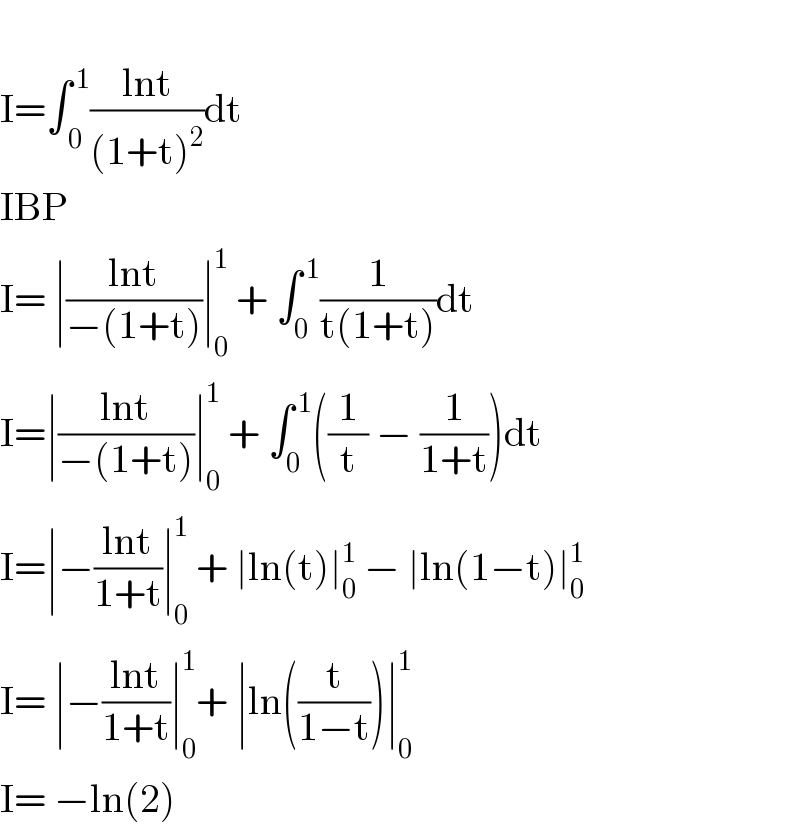
I=∫_( 0) ^( 1) ((lnt)/((1+t)^2 ))dt IBP I= ∣((lnt)/(−(1+t)))∣_0 ^1 + ∫_0 ^( 1) (1/(t(1+t)))dt I=∣((lnt)/(−(1+t)))∣_0 ^1 + ∫_0 ^( 1) ((1/t) − (1/(1+t)))dt I=∣−((lnt)/(1+t))∣_0 ^1 + ∣ln(t)∣_0 ^1 − ∣ln(1−t)∣_0 ^1 I= ∣−((lnt)/(1+t))∣_0 ^1 + ∣ln((t/(1−t)))∣_0 ^1 I= −ln(2)
$$ \\ $$$$\mathrm{I}=\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{IBP} \\ $$$$\mathrm{I}=\:\mid\frac{\mathrm{lnt}}{−\left(\mathrm{1}+\mathrm{t}\right)}\mid_{\mathrm{0}} ^{\mathrm{1}} \:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{t}\left(\mathrm{1}+\mathrm{t}\right)}\mathrm{dt} \\ $$$$\mathrm{I}=\mid\frac{\mathrm{lnt}}{−\left(\mathrm{1}+\mathrm{t}\right)}\mid_{\mathrm{0}} ^{\mathrm{1}} \:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{t}}\:−\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}}\right)\mathrm{dt} \\ $$$$\mathrm{I}=\mid−\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}}\mid_{\mathrm{0}} ^{\mathrm{1}} \:+\:\mid\mathrm{ln}\left(\mathrm{t}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \:−\:\mid\mathrm{ln}\left(\mathrm{1}−\mathrm{t}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}=\:\mid−\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}}\mid_{\mathrm{0}} ^{\mathrm{1}} +\:\mid\mathrm{ln}\left(\frac{\mathrm{t}}{\mathrm{1}−\mathrm{t}}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}=\:−\mathrm{ln}\left(\mathrm{2}\right) \\ $$
Commented by SOMEDAVONG last updated on 31/Oct/20
(Thank you so much)
$$\left(\boldsymbol{\mathrm{Thank}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{much}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *