Question Number 130290 by bramlexs22 last updated on 24/Jan/21
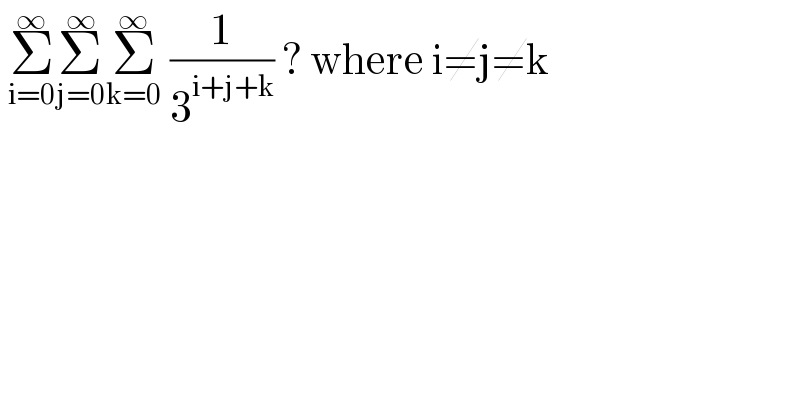
$$\:\underset{\mathrm{i}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{j}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{i}+\mathrm{j}+\mathrm{k}} }\:?\:\mathrm{where}\:\mathrm{i}\neq\mathrm{j}\neq\mathrm{k} \\ $$
Answered by EDWIN88 last updated on 24/Jan/21
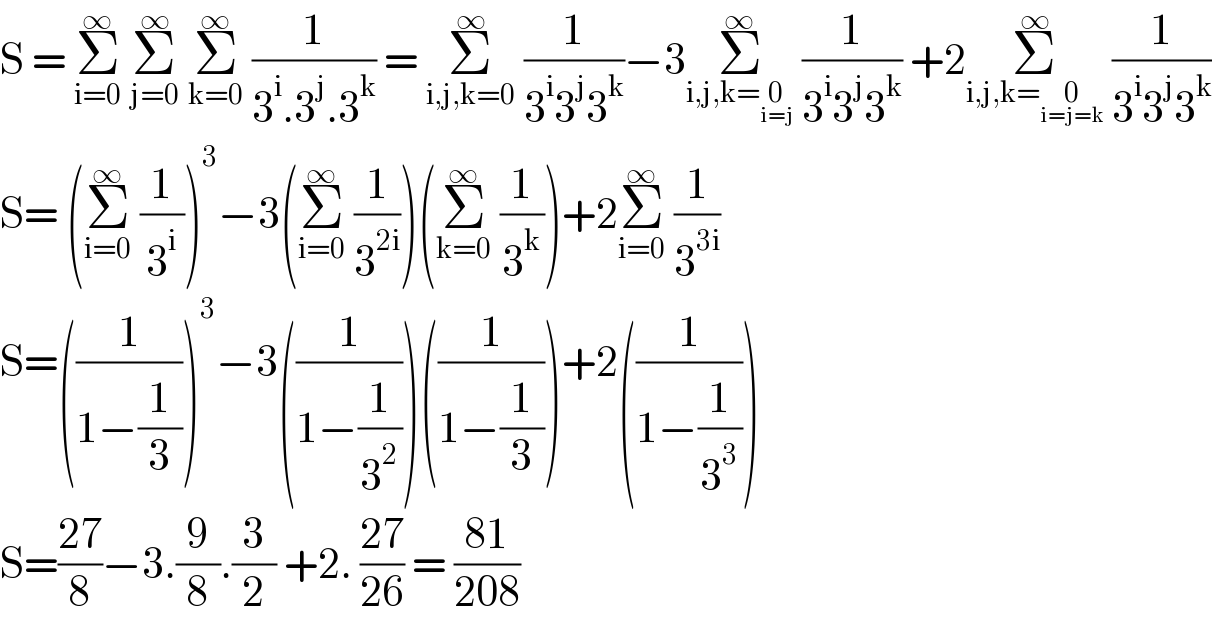
$$\mathrm{S}\:=\:\underset{\mathrm{i}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{\mathrm{j}=\mathrm{0}} {\overset{\infty} {\sum}}\:\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{i}} .\mathrm{3}^{\mathrm{j}} .\mathrm{3}^{\mathrm{k}} }\:=\:\underset{\mathrm{i},\mathrm{j},\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{i}} \mathrm{3}^{\mathrm{j}} \mathrm{3}^{\mathrm{k}} }−\mathrm{3}\underset{\mathrm{i},\mathrm{j},\mathrm{k}=\underset{\mathrm{i}=\mathrm{j}} {\mathrm{0}}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{i}} \mathrm{3}^{\mathrm{j}} \mathrm{3}^{\mathrm{k}} }\:+\mathrm{2}\underset{\mathrm{i},\mathrm{j},\mathrm{k}=\underset{\mathrm{i}=\mathrm{j}=\mathrm{k}} {\mathrm{0}}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{i}} \mathrm{3}^{\mathrm{j}} \mathrm{3}^{\mathrm{k}} } \\ $$$$\mathrm{S}=\:\left(\underset{\mathrm{i}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{i}} }\right)^{\mathrm{3}} −\mathrm{3}\left(\underset{\mathrm{i}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2i}} }\right)\left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{k}} }\right)+\mathrm{2}\underset{\mathrm{i}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3i}} } \\ $$$$\mathrm{S}=\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\mathrm{3}} −\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}} }}\right)\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}\right)+\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }}\right) \\ $$$$\mathrm{S}=\frac{\mathrm{27}}{\mathrm{8}}−\mathrm{3}.\frac{\mathrm{9}}{\mathrm{8}}.\frac{\mathrm{3}}{\mathrm{2}}\:+\mathrm{2}.\:\frac{\mathrm{27}}{\mathrm{26}}\:=\:\frac{\mathrm{81}}{\mathrm{208}} \\ $$
