Question Number 129710 by SOMEDAVONG last updated on 18/Jan/21
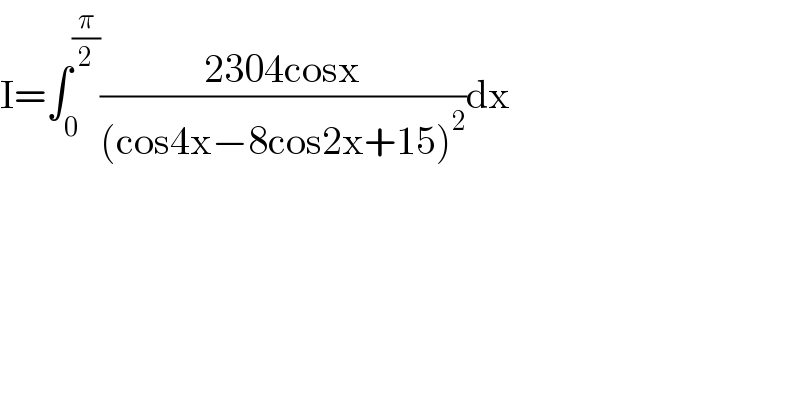
$$\mathrm{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2304cosx}}{\left(\mathrm{cos4x}−\mathrm{8cos2x}+\mathrm{15}\right)^{\mathrm{2}} }\mathrm{dx}\: \\ $$
Answered by MJS_new last updated on 18/Jan/21
![2304∫((cos x)/((cos 4x −8cos 2x +15)^2 ))dx= [t=sin x → dx=(dt/(cos x))] =36∫(dt/((t^2 −t+1)^2 (t^2 +t+1)^2 ))= [Ostrogradski′s Method] =−((6t(t−1)(t+1))/((t^2 −t+1)(t^2 +t+1)))−6∫((t^2 −5)/((t^2 −t+1)(t^2 +t+1)))dt −6∫((t^2 −5)/((t^2 −t+1)(t^2 +t+1)))dt= =−3∫((6t−5)/(t^2 −t+1))dt+3∫((6t+5)/(t^2 +t+1))dt= =6∫(dt/(t^2 −t+1))−9∫((2t−1)/(t^2 −t+1))dt+6∫(dt/(t^2 +t+1))+9∫((2t+1)/(t^2 +t+1))dt= =4(√3)arctan (((√3)(2t−1))/3) −9ln (t^2 −t+1) +4(√3)arctan (((√3)(2t+1))/3) +9ln (t^2 +t+1) ⇒ we have 2304∫_0 ^(π/2) ((cos x)/((cos 4x −8cos 2x +15)^2 ))dx= [−((6t(t−1)(t+1))/((t^2 −t+1)(t^2 +t+1)))+4(√3)(arctan (((√3)(2t−1))/3) +arctan (((√3)(2t+1))/3))+9ln ((t^2 +t+1)/(t^2 −t+1))]_0 ^1 = =2π(√3)+9ln 3](https://www.tinkutara.com/question/Q129724.png)
$$\mathrm{2304}\int\frac{\mathrm{cos}\:{x}}{\left(\mathrm{cos}\:\mathrm{4}{x}\:−\mathrm{8cos}\:\mathrm{2}{x}\:+\mathrm{15}\right)^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{cos}\:{x}}\right] \\ $$$$=\mathrm{36}\int\frac{{dt}}{\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{\mathrm{6}{t}\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}−\mathrm{6}\int\frac{{t}^{\mathrm{2}} −\mathrm{5}}{\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{dt} \\ $$$$−\mathrm{6}\int\frac{{t}^{\mathrm{2}} −\mathrm{5}}{\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}{dt}= \\ $$$$=−\mathrm{3}\int\frac{\mathrm{6}{t}−\mathrm{5}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{dt}+\mathrm{3}\int\frac{\mathrm{6}{t}+\mathrm{5}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}= \\ $$$$=\mathrm{6}\int\frac{{dt}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}−\mathrm{9}\int\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{dt}+\mathrm{6}\int\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}+\mathrm{9}\int\frac{\mathrm{2}{t}+\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{dt}= \\ $$$$=\mathrm{4}\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{3}}\:−\mathrm{9ln}\:\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\:+\mathrm{4}\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}}\:+\mathrm{9ln}\:\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right) \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{2304}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{cos}\:{x}}{\left(\mathrm{cos}\:\mathrm{4}{x}\:−\mathrm{8cos}\:\mathrm{2}{x}\:+\mathrm{15}\right)^{\mathrm{2}} }{dx}= \\ $$$$\left[−\frac{\mathrm{6}{t}\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)}{\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)}+\mathrm{4}\sqrt{\mathrm{3}}\left(\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}−\mathrm{1}\right)}{\mathrm{3}}\:+\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{t}+\mathrm{1}\right)}{\mathrm{3}}\right)+\mathrm{9ln}\:\frac{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$=\mathrm{2}\pi\sqrt{\mathrm{3}}+\mathrm{9ln}\:\mathrm{3} \\ $$
