Question Number 87815 by jagoll last updated on 06/Apr/20

$$\mathrm{I}\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\mathrm{cos}\:\mathrm{2x}\left(\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}\right)\:\mathrm{dx} \\ $$
Commented by john santu last updated on 06/Apr/20
![cos^4 x+sin^4 x = (cos^2 x+sin^2 x)^2 −2cos^2 xsin^2 x = 1 − (1/2)sin^2 (2x) I=∫(1/2) cos 2x (2−sin^2 (2x))dx [let t = sin 2x ⇒ dt = 2cos 2x dx] I = (1/4)∫ (2−t^2 ) dt I = (1/4)[ 2t −(1/3)t^3 ] now I = (1/4)[ 2sin 2x−(1/3)sin^3 2x ]_0 ^(π/2) I = 0](https://www.tinkutara.com/question/Q87819.png)
$$\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}\:=\:\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} −\mathrm{2cos}\:^{\mathrm{2}} \mathrm{xsin}\:^{\mathrm{2}} \mathrm{x} \\ $$$$=\:\mathrm{1}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{2x}\right) \\ $$$$\mathrm{I}=\int\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{2x}\:\left(\mathrm{2}−\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{2x}\right)\right)\mathrm{dx} \\ $$$$\left[\mathrm{let}\:\mathrm{t}\:=\:\mathrm{sin}\:\mathrm{2x}\:\Rightarrow\:\mathrm{dt}\:=\:\mathrm{2cos}\:\mathrm{2x}\:\mathrm{dx}\right] \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\left(\mathrm{2}−\mathrm{t}^{\mathrm{2}} \right)\:\mathrm{dt} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:\mathrm{2t}\:−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\mathrm{3}} \right]\: \\ $$$$\mathrm{now}\:\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\:\mathrm{2sin}\:\mathrm{2x}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}\:^{\mathrm{3}} \mathrm{2x}\:\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{I}\:=\:\mathrm{0} \\ $$
Commented by jagoll last updated on 06/Apr/20

$$\mathrm{thank}\:\mathrm{sir} \\ $$
Commented by mathmax by abdo last updated on 06/Apr/20
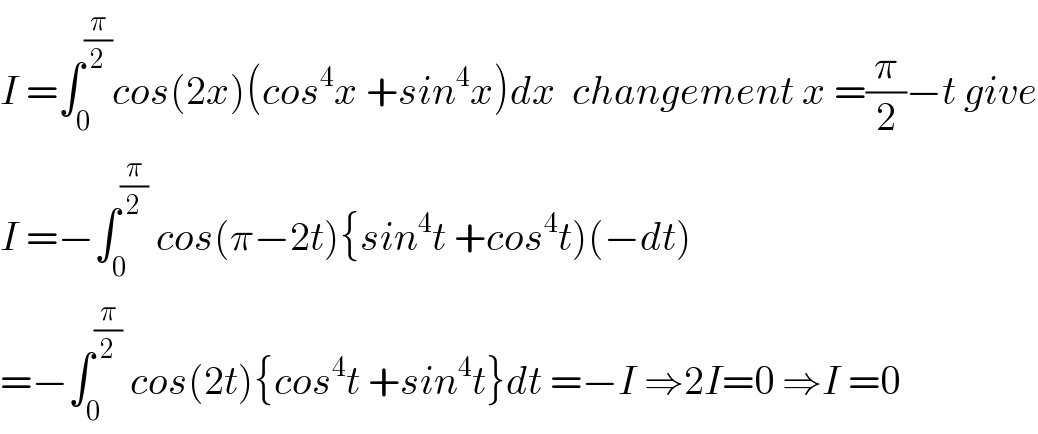
$${I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{x}\right)\left({cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}\right){dx}\:\:{changement}\:{x}\:=\frac{\pi}{\mathrm{2}}−{t}\:{give} \\ $$$${I}\:=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\pi−\mathrm{2}{t}\right)\left\{{sin}^{\mathrm{4}} {t}\:+{cos}^{\mathrm{4}} {t}\right)\left(−{dt}\right) \\ $$$$=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{t}\right)\left\{{cos}^{\mathrm{4}} {t}\:+{sin}^{\mathrm{4}} {t}\right\}{dt}\:=−{I}\:\Rightarrow\mathrm{2}{I}=\mathrm{0}\:\Rightarrow{I}\:=\mathrm{0} \\ $$
Answered by redmiiuser last updated on 06/Apr/20
![sin^4 x+cos^4 x =(sin^2 x+cos^2 x)^2 −2sin^2 x.cos^2 x =1−2.(((sin 2x)^2 )/4) =1−((1−cos 4x)/4) =((3+cos 4x)/4) ∫_0 ^(π/2) ((3/4)cos 2x.dx+(1/4)cos 2x.cos 4x.dx) =(3/8)[sin 2x]_0 ^(π/2) +(1/8)[((sin 6x)/6)]_0 ^(π/2) +(1/8)[((sin 2x)/2)]_0 ^(π/2) =0](https://www.tinkutara.com/question/Q87830.png)
$$\mathrm{sin}\:^{\mathrm{4}} {x}+\mathrm{cos}\:^{\mathrm{4}} {x} \\ $$$$=\left(\mathrm{sin}\:^{\mathrm{2}} {x}+\mathrm{cos}\:^{\mathrm{2}} {x}\right)^{\mathrm{2}} −\mathrm{2sin}\:^{\mathrm{2}} {x}.\mathrm{cos}\:^{\mathrm{2}} {x} \\ $$$$=\mathrm{1}−\mathrm{2}.\frac{\left(\mathrm{sin}\:\mathrm{2}{x}\right)^{\mathrm{2}} }{\mathrm{4}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{3}+\mathrm{cos}\:\mathrm{4}{x}}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}\:\mathrm{2}{x}.{dx}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{2}{x}.\mathrm{cos}\:\mathrm{4}{x}.{dx}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{8}}\left[\mathrm{sin}\:\mathrm{2}{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{8}}\left[\frac{{sin}\:\mathrm{6}{x}}{\mathrm{6}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\frac{\mathrm{1}}{\mathrm{8}}\left[\frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{0} \\ $$
