Question Number 162604 by amin96 last updated on 30/Dec/21
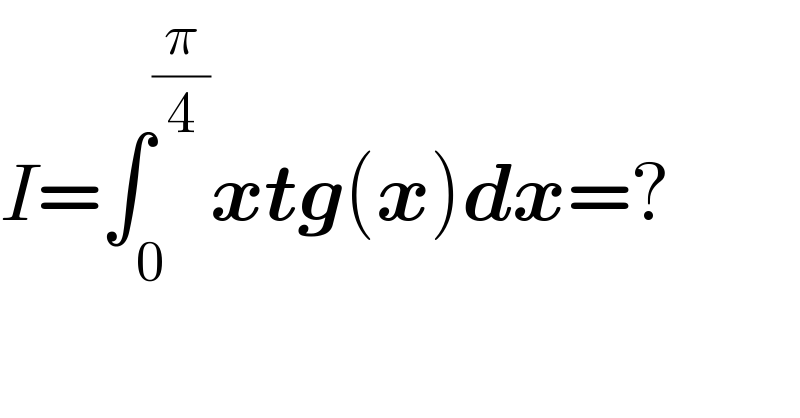
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \boldsymbol{{xtg}}\left(\boldsymbol{{x}}\right)\boldsymbol{{dx}}=? \\ $$
Answered by Ar Brandon last updated on 30/Dec/21
![I=∫_0 ^(π/4) xtanxdx =−[xln(cosx)]_0 ^(π/4) +∫_0 ^(π/4) ln(cosx)dx =−(π/4)ln((1/( (√2))))+(G/2)−((πln2)/4)=(G/2)−((πln2)/8)](https://www.tinkutara.com/question/Q162609.png)
$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}\mathrm{tan}{xdx} \\ $$$$\:\:\:=−\left[{x}\mathrm{ln}\left(\mathrm{cos}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{cos}{x}\right){dx} \\ $$$$\:\:\:=−\frac{\pi}{\mathrm{4}}\mathrm{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)+\frac{{G}}{\mathrm{2}}−\frac{\pi\mathrm{ln2}}{\mathrm{4}}=\frac{{G}}{\mathrm{2}}−\frac{\pi\mathrm{ln2}}{\mathrm{8}} \\ $$
