I-0-tan-1-x-1-x-2-2-dx-

Question Number 162811 by mnjuly1970 last updated on 01/Jan/22

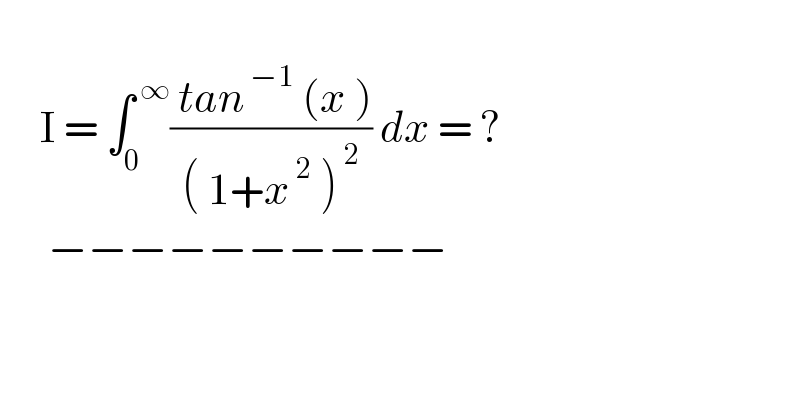
$$ \\ $$$$\:\:\:\:\:\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{tan}^{\:−\mathrm{1}} \:\left({x}\:\right)}{\left(\:\mathrm{1}+{x}^{\:\mathrm{2}} \:\right)^{\:\mathrm{2}} }\:{dx}\:=\:? \\ $$$$\:\:\:\:\:\:−−−−−−−−−− \\ $$

Answered by amin96 last updated on 01/Jan/22

arctg(x)=t x=tg(t) (dt/dx)=(1/(x^2 +1)) t[(π/2):0] I=∫_0 ^(π/2) (t/((1+x^2 )))dt=∫_0 ^(π/2) (t/(1+tg^2 (t)))dt=∫_0 ^(π/2) tcos^2 (t)dt IBP t=u du=dt v=((2t+sin(2t))/4) I=[t((t/2)+((sin(2t))/4))]_0 ^(π/2) −∫_0 ^(π/2) ((t/2)+((sin(2t))/4))dt= =(π^2 /8)−[(t^2 /4)]_0 ^(π/2) −(1/4)∫_0 ^(π/2) sin(2t)dt_(1) =(π^2 /8)−(π^2 /(16))−(1/4)= =(π^2 /(16))−(1/4)

$$ \\ $$$$\boldsymbol{{arctg}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{t}}\:\:\:\:\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{tg}}\left(\boldsymbol{\mathrm{t}}\right)\:\:\:\:\frac{\boldsymbol{{dt}}}{\boldsymbol{{dx}}}=\frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{1}}\:\:\:\:{t}\left[\frac{\pi}{\mathrm{2}}:\mathrm{0}\right] \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\boldsymbol{{t}}}{\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \right)}\boldsymbol{{dt}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\boldsymbol{\mathrm{t}}}{\mathrm{1}+\boldsymbol{\mathrm{tg}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{t}}\right)}\boldsymbol{\mathrm{dt}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \boldsymbol{{tcos}}^{\mathrm{2}} \left(\boldsymbol{{t}}\right)\boldsymbol{{dt}} \\ $$$$\boldsymbol{\mathrm{IBP}}\:\boldsymbol{{t}}=\boldsymbol{{u}}\:\:\:\:\boldsymbol{{du}}=\boldsymbol{{dt}}\:\:\:\:\boldsymbol{{v}}=\frac{\mathrm{2}\boldsymbol{{t}}+\boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{t}}\right)}{\mathrm{4}} \\ $$$$\boldsymbol{{I}}=\left[\boldsymbol{{t}}\left(\frac{\boldsymbol{{t}}}{\mathrm{2}}+\frac{\boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{t}}\right)}{\mathrm{4}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\frac{\boldsymbol{{t}}}{\mathrm{2}}+\frac{\boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{t}}\right)}{\mathrm{4}}\right)\boldsymbol{{dt}}= \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\left[\frac{\boldsymbol{{t}}^{\mathrm{2}} }{\mathrm{4}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{1}} {\underbrace{\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \boldsymbol{{sin}}\left(\mathrm{2}\boldsymbol{{t}}\right)\boldsymbol{{dt}}}}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}}= \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 01/Jan/22