Question Number 39341 by rahul 19 last updated on 05/Jul/18
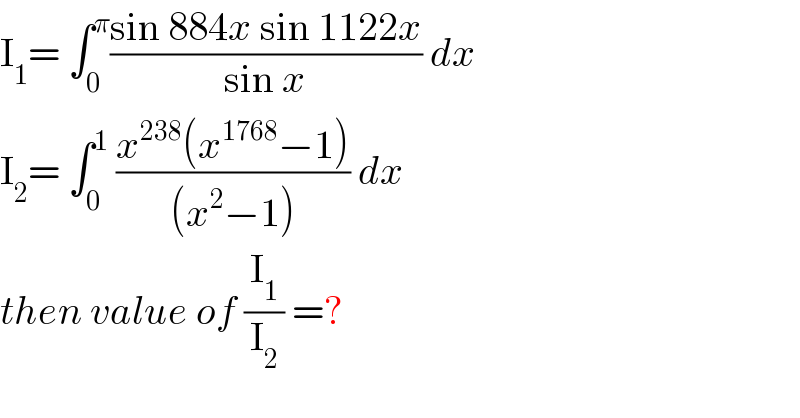
$$\mathrm{I}_{\mathrm{1}} =\:\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{sin}\:\mathrm{884}{x}\:\mathrm{sin}\:\mathrm{1122}{x}}{\mathrm{sin}\:{x}}\:{dx} \\ $$$$\mathrm{I}_{\mathrm{2}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{\mathrm{238}} \left({x}^{\mathrm{1768}} −\mathrm{1}\right)}{\left({x}^{\mathrm{2}} −\mathrm{1}\right)}\:{dx} \\ $$$${then}\:{value}\:{of}\:\frac{\mathrm{I}_{\mathrm{1}} }{\mathrm{I}_{\mathrm{2}} }\:=? \\ $$
Commented by rahul 19 last updated on 06/Jul/18

$$??????? \\ $$
Commented by rahul 19 last updated on 06/Jul/18

$$\mathrm{pls}\:\mathrm{help}….. \\ $$
Commented by ajfour last updated on 06/Jul/18
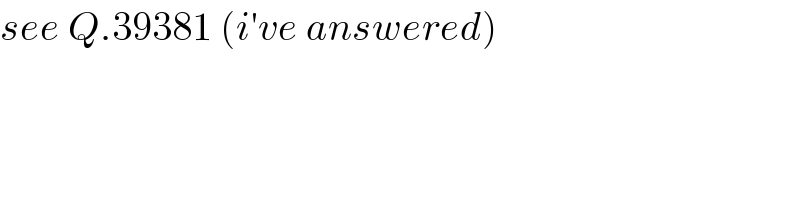
$${see}\:{Q}.\mathrm{39381}\:\left({i}'{ve}\:{answered}\right) \\ $$
Commented by abdo mathsup 649 cc last updated on 07/Jul/18
![I_2 =∫_0 ^1 ((x^(238) ( (x^2 )^(884) −1))/(x^2 −1)) dx = ∫_0 ^1 ((x^(238) (x^2 −1)Σ_(k=0) ^(883) x^(2k) )/(x^2 −1))dx = ∫_0 ^1 Σ_(k=0) ^(883) x^(2k ++238) dx =Σ_(k=0) ^(883) [ (1/(2k +239)) x^(2k +239) ]_0 ^1 ...be continued... =Σ_(k=0) ^(883) (1/(2k +239))](https://www.tinkutara.com/question/Q39570.png)
$${I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{238}} \left(\:\:\left({x}^{\mathrm{2}} \right)^{\mathrm{884}} \:−\mathrm{1}\right)}{{x}^{\mathrm{2}} \:−\mathrm{1}}\:{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{\mathrm{238}} \left({x}^{\mathrm{2}} \:−\mathrm{1}\right)\sum_{{k}=\mathrm{0}} ^{\mathrm{883}} \:\:{x}^{\mathrm{2}{k}} }{{x}^{\mathrm{2}} \:−\mathrm{1}}{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\sum_{{k}=\mathrm{0}} ^{\mathrm{883}} \:\:{x}^{\mathrm{2}{k}\:++\mathrm{238}} {dx} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{883}} \:\:\:\:\:\left[\:\frac{\mathrm{1}}{\mathrm{2}{k}\:+\mathrm{239}}\:{x}^{\mathrm{2}{k}\:+\mathrm{239}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:\:\:…{be}\:{continued}… \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{883}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}{k}\:+\mathrm{239}} \\ $$
