Question Number 184552 by Frix last updated on 08/Jan/23
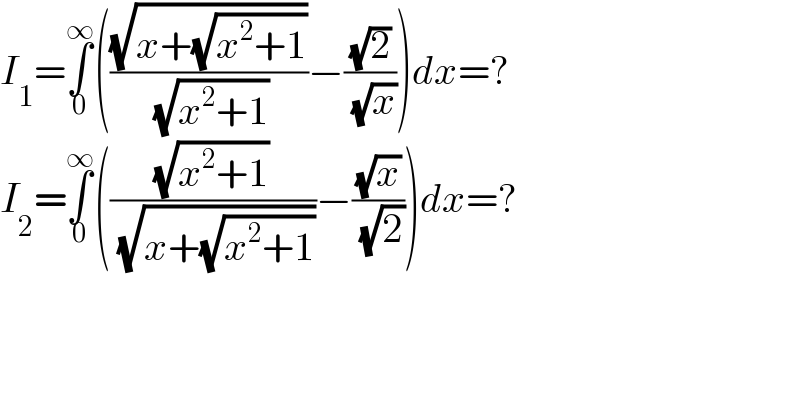
$${I}_{\mathrm{1}} =\underset{\mathrm{0}} {\overset{\infty} {\int}}\left(\frac{\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}−\frac{\sqrt{\mathrm{2}}}{\:\sqrt{{x}}}\right){dx}=? \\ $$$${I}_{\mathrm{2}} =\underset{\mathrm{0}} {\overset{\infty} {\int}}\left(\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}}−\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{2}}}\right){dx}=? \\ $$
Answered by SEKRET last updated on 08/Jan/23

$$\:\:\boldsymbol{\mathrm{t}}\:=\:\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}} \\ $$$$ \\ $$
Commented by Frix last updated on 08/Jan/23
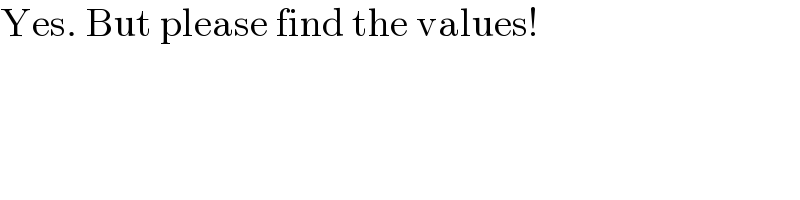
$$\mathrm{Yes}.\:\mathrm{But}\:\mathrm{please}\:\mathrm{find}\:\mathrm{the}\:\mathrm{values}! \\ $$
Answered by SEKRET last updated on 08/Jan/23
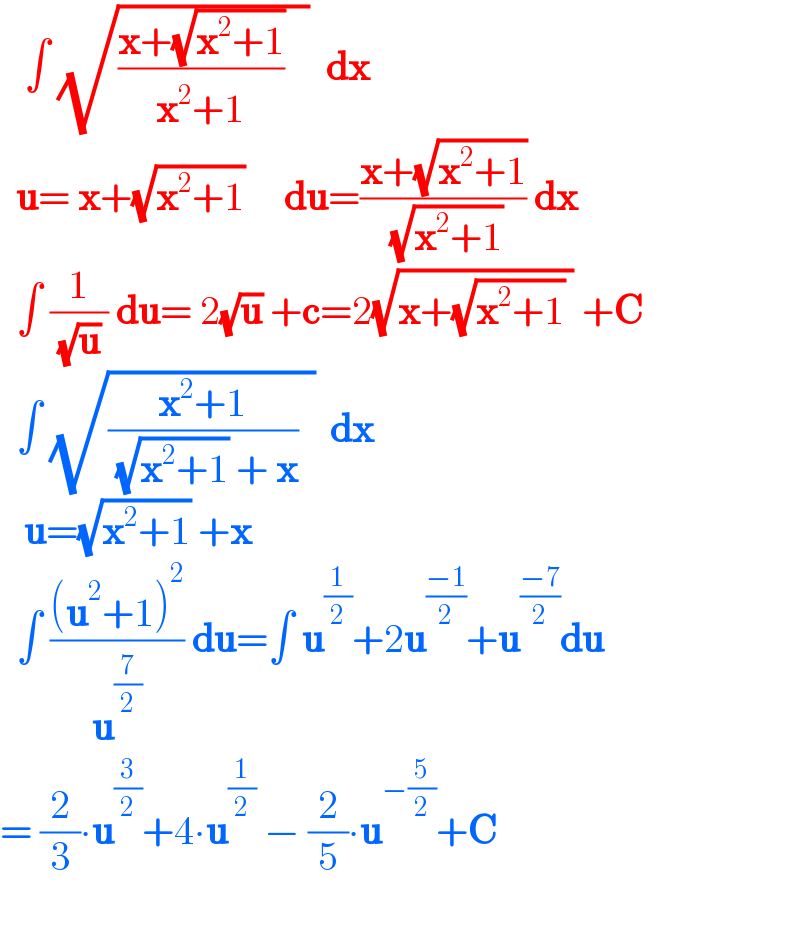
$$\:\:\:\int\:\sqrt{\frac{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}}{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:\:\:}\:\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\:\boldsymbol{\mathrm{u}}=\:\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:\:\:\:\:\boldsymbol{\mathrm{du}}=\frac{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}}\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\:\int\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{\mathrm{u}}}\:}\:\boldsymbol{\mathrm{du}}=\:\mathrm{2}\sqrt{\boldsymbol{\mathrm{u}}}\:+\boldsymbol{\mathrm{c}}=\mathrm{2}\sqrt{\boldsymbol{\mathrm{x}}+\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:}\:+\boldsymbol{\mathrm{C}} \\ $$$$\:\:\int\:\sqrt{\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}{\:\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:+\:\boldsymbol{\mathrm{x}}}\:\:}\:\:\boldsymbol{\mathrm{dx}} \\ $$$$\:\:\:\boldsymbol{\mathrm{u}}=\sqrt{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{1}}\:+\boldsymbol{\mathrm{x}} \\ $$$$\:\:\int\:\frac{\left(\boldsymbol{\mathrm{u}}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\boldsymbol{\mathrm{u}}^{\frac{\mathrm{7}}{\mathrm{2}}} }\:\boldsymbol{\mathrm{du}}=\int\:\boldsymbol{\mathrm{u}}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{2}\boldsymbol{\mathrm{u}}^{\frac{−\mathrm{1}}{\mathrm{2}}} +\boldsymbol{\mathrm{u}}^{\frac{−\mathrm{7}}{\mathrm{2}}} \boldsymbol{\mathrm{du}} \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{3}}\centerdot\boldsymbol{\mathrm{u}}^{\frac{\mathrm{3}}{\mathrm{2}}} +\mathrm{4}\centerdot\boldsymbol{\mathrm{u}}^{\frac{\mathrm{1}}{\mathrm{2}}} \:−\:\frac{\mathrm{2}}{\mathrm{5}}\centerdot\boldsymbol{\mathrm{u}}^{−\frac{\mathrm{5}}{\mathrm{2}}} +\boldsymbol{\mathrm{C}} \\ $$$$ \\ $$
