Question Number 146521 by mathdanisur last updated on 13/Jul/21
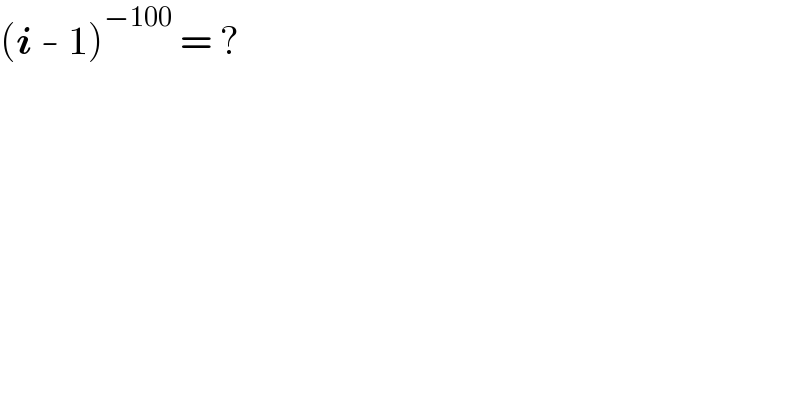
$$\left(\boldsymbol{{i}}\:-\:\mathrm{1}\right)^{−\mathrm{100}} \:=\:? \\ $$
Answered by mathmax by abdo last updated on 13/Jul/21
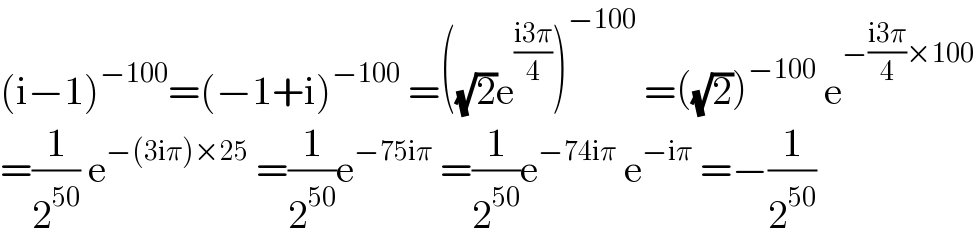
$$\left(\mathrm{i}−\mathrm{1}\right)^{−\mathrm{100}} =\left(−\mathrm{1}+\mathrm{i}\right)^{−\mathrm{100}} \:=\left(\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{i3}\pi}{\mathrm{4}}} \right)^{−\mathrm{100}} \:=\left(\sqrt{\mathrm{2}}\right)^{−\mathrm{100}} \:\mathrm{e}^{−\frac{\mathrm{i3}\pi}{\mathrm{4}}×\mathrm{100}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{50}} }\:\mathrm{e}^{−\left(\mathrm{3i}\pi\right)×\mathrm{25}} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{50}} }\mathrm{e}^{−\mathrm{75i}\pi} \:=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{50}} }\mathrm{e}^{−\mathrm{74i}\pi} \:\mathrm{e}^{−\mathrm{i}\pi} \:=−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{50}} } \\ $$
Commented by mathdanisur last updated on 13/Jul/21

$${thank}\:{you}\:{Ser} \\ $$
