Question Number 103253 by Study last updated on 13/Jul/20

$$\:\sqrt[{{i}}]{{i}}=????? \\ $$
Answered by Dwaipayan Shikari last updated on 13/Jul/20

$${i}^{\frac{\mathrm{1}}{{i}}} ={i}^{−{i}} \:\:\:\:\left(\frac{\mathrm{1}}{{i}}=\frac{{i}}{{i}^{\mathrm{2}} }=−{i}\right) \\ $$$${e}^{\pi{i}} =−\mathrm{1} \\ $$$${e}^{\frac{\pi{i}\:}{\mathrm{2}}} ={i} \\ $$$${e}^{\frac{\pi{i}}{\mathrm{2}}.\left(−{i}\right)} ={i}^{−{i}} \\ $$$${e}^{\frac{\pi}{\mathrm{2}}} ={i}^{−{i}} \Rightarrow\mathrm{4}.\mathrm{81077}… \\ $$$$\mathrm{For}\:\mathrm{regularaization} \\ $$$$\mathrm{e}^{\frac{\pi}{\mathrm{2}}+\mathrm{2}\pi\mathrm{k}} \left(\mathrm{k}\in\mathbb{Z}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jul/20
approximately 4.810477380965351655473035666703833126390170874664534940020...
(using the principal branch of the logarithm for complex exponentiation)
Commented by Study last updated on 13/Jul/20
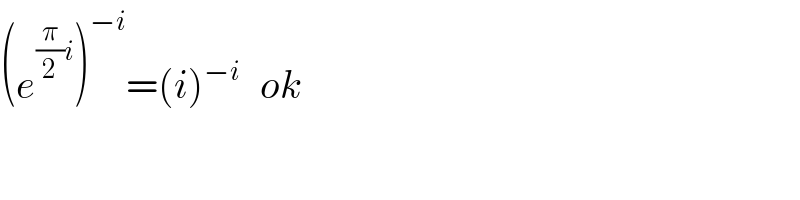
$$\left({e}^{\frac{\pi}{\mathrm{2}}{i}} \right)^{−{i}} =\left({i}\right)^{−{i}\:\:\:\:\:} {ok} \\ $$
Commented by Study last updated on 13/Jul/20

$$\frac{\mathrm{1}}{{i}}={i}^{−\mathrm{1}} \:\:\:\:\:{ok} \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jul/20

$$\frac{\mathrm{1}}{{i}}=\frac{{i}}{{i}^{\mathrm{2}} }=−{i} \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jul/20

$${it}\:{means}\: \\ $$$${e}^{\frac{\pi}{\mathrm{2}}{i}.\left(−{i}\right)} =\left({i}\right)^{−{i}} \\ $$
Answered by abdomsup last updated on 13/Jul/20
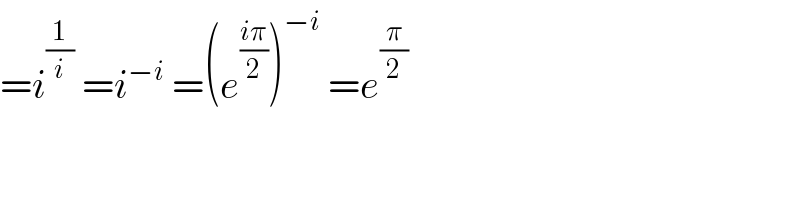
$$={i}^{\frac{\mathrm{1}}{{i}}} \:={i}^{−{i}} \:=\left({e}^{\frac{{i}\pi}{\mathrm{2}}} \right)^{−{i}} \:={e}^{\frac{\pi}{\mathrm{2}}} \\ $$
Answered by OlafThorendsen last updated on 13/Jul/20
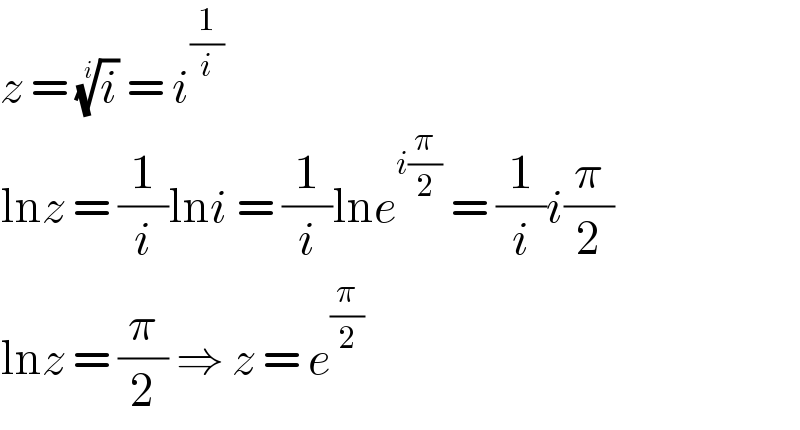
$${z}\:=\:\sqrt[{{i}}]{{i}}\:=\:{i}^{\frac{\mathrm{1}}{{i}}} \\ $$$$\mathrm{ln}{z}\:=\:\frac{\mathrm{1}}{{i}}\mathrm{ln}{i}\:=\:\frac{\mathrm{1}}{{i}}\mathrm{ln}{e}^{{i}\frac{\pi}{\mathrm{2}}} \:=\:\frac{\mathrm{1}}{{i}}{i}\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{ln}{z}\:=\:\frac{\pi}{\mathrm{2}}\:\Rightarrow\:{z}\:=\:{e}^{\frac{\pi}{\mathrm{2}}} \\ $$
