Menu Close

I-1-x-4-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 86703 by lémùst last updated on 30/Mar/20
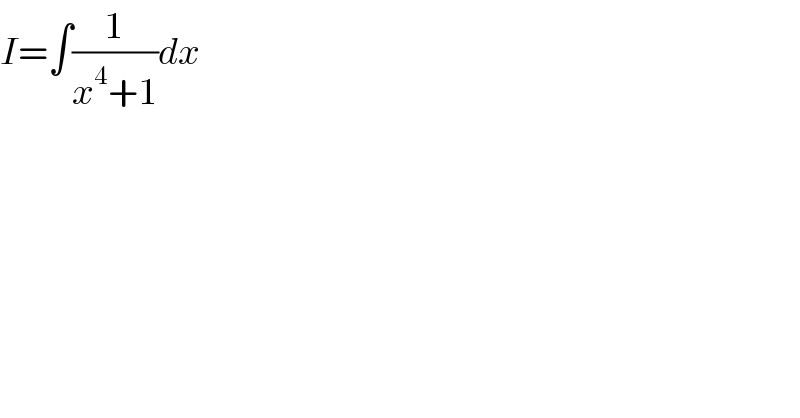
I=∫(1/(x^4 +1))dx
$${I}=\int\frac{\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{1}}{dx} \\ $$
Commented by john santu last updated on 30/Mar/20
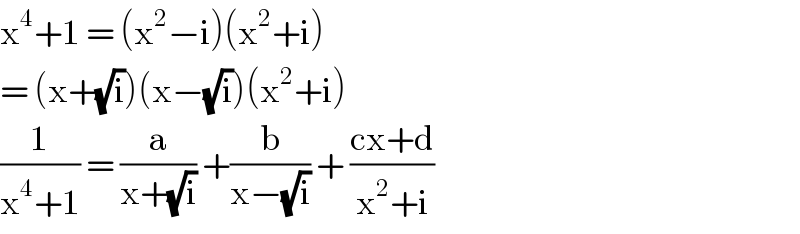
x^4 +1 = (x^2 −i)(x^2 +i) = (x+(√i))(x−(√i))(x^2 +i) (1/(x^4 +1)) = (a/(x+(√i))) +(b/(x−(√i))) + ((cx+d)/(x^2 +i))
$$\mathrm{x}^{\mathrm{4}} +\mathrm{1}\:=\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{i}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{i}\right) \\ $$$$=\:\left(\mathrm{x}+\sqrt{\mathrm{i}}\right)\left(\mathrm{x}−\sqrt{\mathrm{i}}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{i}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}\:=\:\frac{\mathrm{a}}{\mathrm{x}+\sqrt{\mathrm{i}}}\:+\frac{\mathrm{b}}{\mathrm{x}−\sqrt{\mathrm{i}}}\:+\:\frac{\mathrm{cx}+\mathrm{d}}{\mathrm{x}^{\mathrm{2}} +\mathrm{i}}\: \\ $$
Commented by mathmax by abdo last updated on 30/Mar/20
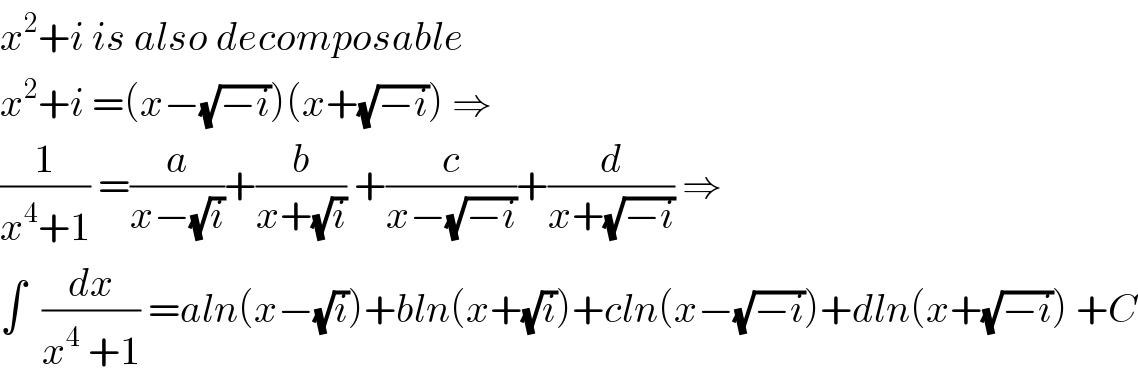
x^2 +i is also decomposable x^2 +i =(x−(√(−i)))(x+(√(−i))) ⇒ (1/(x^4 +1)) =(a/(x−(√i)))+(b/(x+(√i))) +(c/(x−(√(−i))))+(d/(x+(√(−i)))) ⇒ ∫ (dx/(x^4 +1)) =aln(x−(√i))+bln(x+(√i))+cln(x−(√(−i)))+dln(x+(√(−i))) +C
$${x}^{\mathrm{2}} +{i}\:{is}\:{also}\:{decomposable}\: \\ $$$${x}^{\mathrm{2}} +{i}\:=\left({x}−\sqrt{−{i}}\right)\left({x}+\sqrt{−{i}}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{1}}\:=\frac{{a}}{{x}−\sqrt{{i}}}+\frac{{b}}{{x}+\sqrt{{i}}}\:+\frac{{c}}{{x}−\sqrt{−{i}}}+\frac{{d}}{{x}+\sqrt{−{i}}}\:\Rightarrow \\ $$$$\int\:\:\frac{{dx}}{{x}^{\mathrm{4}} \:+\mathrm{1}}\:={aln}\left({x}−\sqrt{{i}}\right)+{bln}\left({x}+\sqrt{{i}}\right)+{cln}\left({x}−\sqrt{−{i}}\right)+{dln}\left({x}+\sqrt{−{i}}\right)\:+{C} \\ $$
Commented by Ar Brandon last updated on 30/Mar/20
I=(1/2)∫((x^2 +1)/(x^4 +1))dx−(1/2)∫((x^2 −1)/(x^4 +1))dx =(1/2)∫((1+(1/x^2 ))/(x^2 +(1/x^2 )))dx−(1/2)∫((1−(1/x^2 ))/(x^2 +(1/x^2 )))dx =(1/2)∫((1+(1/x^2 ))/(2+(x−(1/x))^2 ))dx−(1/2)∫((1−(1/x^2 ))/((x+(1/x))^2 −2))dx let u=x−(1/x) and v=x+(1/x) ⇒I=(1/2)∫(du/(2+u^2 ))−(1/2)∫(dv/(v^2 −2)) =((√2)/4)arctan ((u/( (√2))))+((√2)/4)arcoth ((v/( (√2)))) I=((√2)/4)arctan((1/( (√2)))(x−(1/x)))+((√2)/4)arcoth((1/( (√2)))(x+(1/x)))+C C∈R
$$\boldsymbol{{I}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{1}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{4}} +\mathrm{1}}{dx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{dx} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\mathrm{2}+\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} }{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}}{dx} \\ $$$$\:{let}\:\:{u}={x}−\frac{\mathrm{1}}{{x}}\:\:\:\:\:{and}\:\:\:\:{v}={x}+\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow\boldsymbol{{I}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{\mathrm{2}+{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dv}}{{v}^{\mathrm{2}} −\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{arctan}\:\left(\frac{{u}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{arcoth}\:\left(\frac{{v}}{\:\sqrt{\mathrm{2}}}\right) \\ $$$$\boldsymbol{{I}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left({x}−\frac{\mathrm{1}}{{x}}\right)\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}{arcoth}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left({x}+\frac{\mathrm{1}}{{x}}\right)\right)+{C} \\ $$$$\:\:{C}\in\mathbb{R} \\ $$
Commented by lémùst last updated on 31/Mar/20
thanks
$${thanks} \\ $$
Commented by lémùst last updated on 31/Mar/20
I don′t understand
$${I}\:{don}'{t}\:{understand} \\ $$
Commented by Ar Brandon last updated on 31/Mar/20
At what level?
$$\mathscr{A}{t}\:{what}\:{level}? \\ $$
Answered by MJS last updated on 30/Mar/20
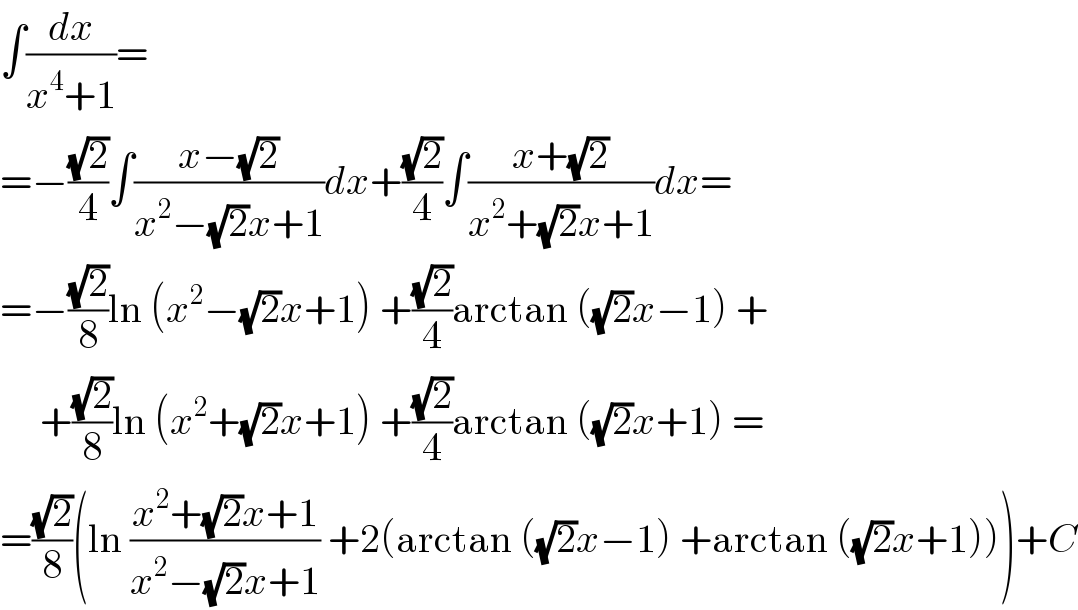
∫(dx/(x^4 +1))= =−((√2)/4)∫((x−(√2))/(x^2 −(√2)x+1))dx+((√2)/4)∫((x+(√2))/(x^2 +(√2)x+1))dx= =−((√2)/8)ln (x^2 −(√2)x+1) +((√2)/4)arctan ((√2)x−1) + +((√2)/8)ln (x^2 +(√2)x+1) +((√2)/4)arctan ((√2)x+1) = =((√2)/8)(ln ((x^2 +(√2)x+1)/(x^2 −(√2)x+1)) +2(arctan ((√2)x−1) +arctan ((√2)x+1)))+C
$$\int\frac{{dx}}{{x}^{\mathrm{4}} +\mathrm{1}}= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{x}−\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}+\mathrm{1}}{dx}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\int\frac{{x}+\sqrt{\mathrm{2}}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}{x}+\mathrm{1}}{dx}= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}+\mathrm{1}\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}−\mathrm{1}\right)\:+ \\ $$$$\:\:\:\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\mathrm{ln}\:\left({x}^{\mathrm{2}} +\sqrt{\mathrm{2}}{x}+\mathrm{1}\right)\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}+\mathrm{1}\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{8}}\left(\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{2}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{2}}{x}+\mathrm{1}}\:+\mathrm{2}\left(\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}−\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{x}+\mathrm{1}\right)\right)\right)+{C} \\ $$
Commented by lémùst last updated on 31/Mar/20
thanks
$${thanks} \\ $$
Answered by TANMAY PANACEA. last updated on 30/Mar/20
∫(dx/(x^2 (x^2 +(1/x^2 )))) (1/2)∫(((1+(1/x^2 ))−(1−(1/x^2 )))/((x^2 +(1/x^2 ))))dx (1/2)∫((d(x−(1/x)))/((x−(1/x))^2 +2))−(1/2)∫((d(x+(1/x)))/((x+(1/x))^2 −2)) now use formula ∫(dx/(x^2 +a^2 ))=(1/a)tan^(−1) ((x/a))+c_1 ∫(dx/(x^2 −a^2 ))=(1/(2a))∫((1/(x−a))−(1/(x+a)))dx=(1/(2a))ln(((x−a)/(x+a)))+c_2 (1/2)×(1/( (√2)))tan^(−1) (((x−(1/x))/( (√2))))−(1/2)×(1/(2(√2)))ln(((x+(1/x)−(√2))/(x+(1/x)+(√2))))+C
$$\int\frac{{dx}}{{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)−\left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$${now}\:{use}\:{formula}\:\int\frac{{dx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{{a}}{tan}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)+{c}_{\mathrm{1}} \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}{a}}\int\left(\frac{\mathrm{1}}{{x}−{a}}−\frac{\mathrm{1}}{{x}+{a}}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\left(\frac{{x}−{a}}{{x}+{a}}\right)+{c}_{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\:\sqrt{\mathrm{2}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}{ln}\left(\frac{{x}+\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{2}}}{{x}+\frac{\mathrm{1}}{{x}}+\sqrt{\mathrm{2}}}\right)+{C} \\ $$$$ \\ $$$$ \\ $$
Commented by lémùst last updated on 31/Mar/20
thanks
$${thanks} \\ $$
Answered by redmiiuser last updated on 01/Apr/20
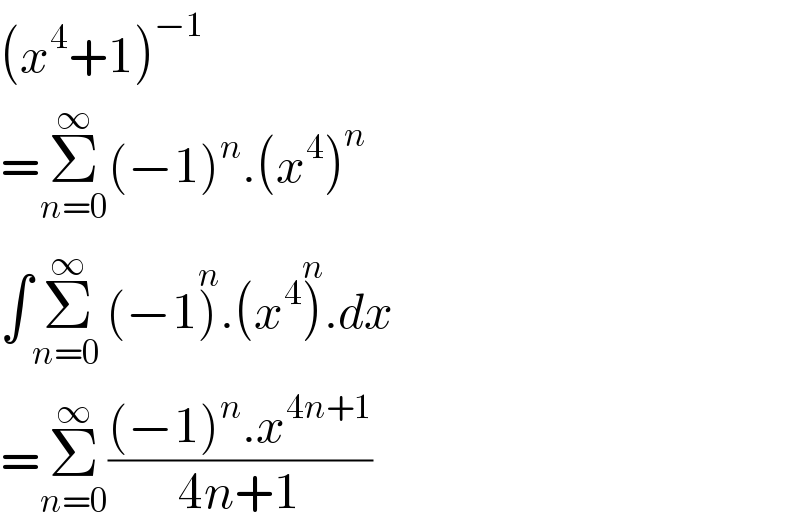
(x^4 +1)^(−1) =Σ_(n=0) ^∞ (−1)^n .(x^4 )^n ∫Σ_(n=0 ) ^∞ (−1)^n .(x^4 )^n .dx =Σ_(n=0) ^∞ (((−1)^n .x^(4n+1) )/(4n+1))
$$\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{−\mathrm{1}} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .\left({x}^{\mathrm{4}} \right)^{{n}} \\ $$$$\int\underset{{n}=\mathrm{0}\:} {\overset{\infty} {\sum}}\left(−\mathrm{1}\overset{{n}} {\right)}.\left({x}^{\mathrm{4}} \overset{{n}} {\right)}.{dx} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} .{x}^{\mathrm{4}{n}+\mathrm{1}} }{\mathrm{4}{n}+\mathrm{1}} \\ $$
Commented by redmiiuser last updated on 01/Apr/20
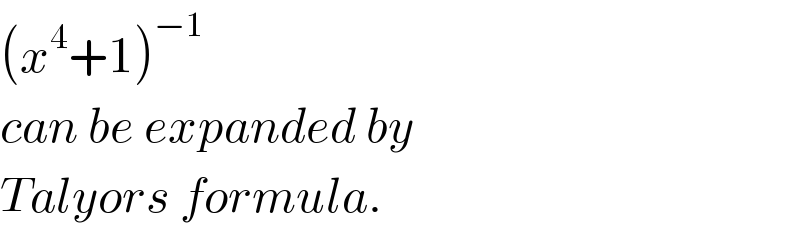
(x^4 +1)^(−1) can be expanded by Talyors formula.
$$\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{−\mathrm{1}} \\ $$$${can}\:{be}\:{expanded}\:{by} \\ $$$${Talyors}\:{formula}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *