Question Number 182954 by Gamil last updated on 17/Dec/22
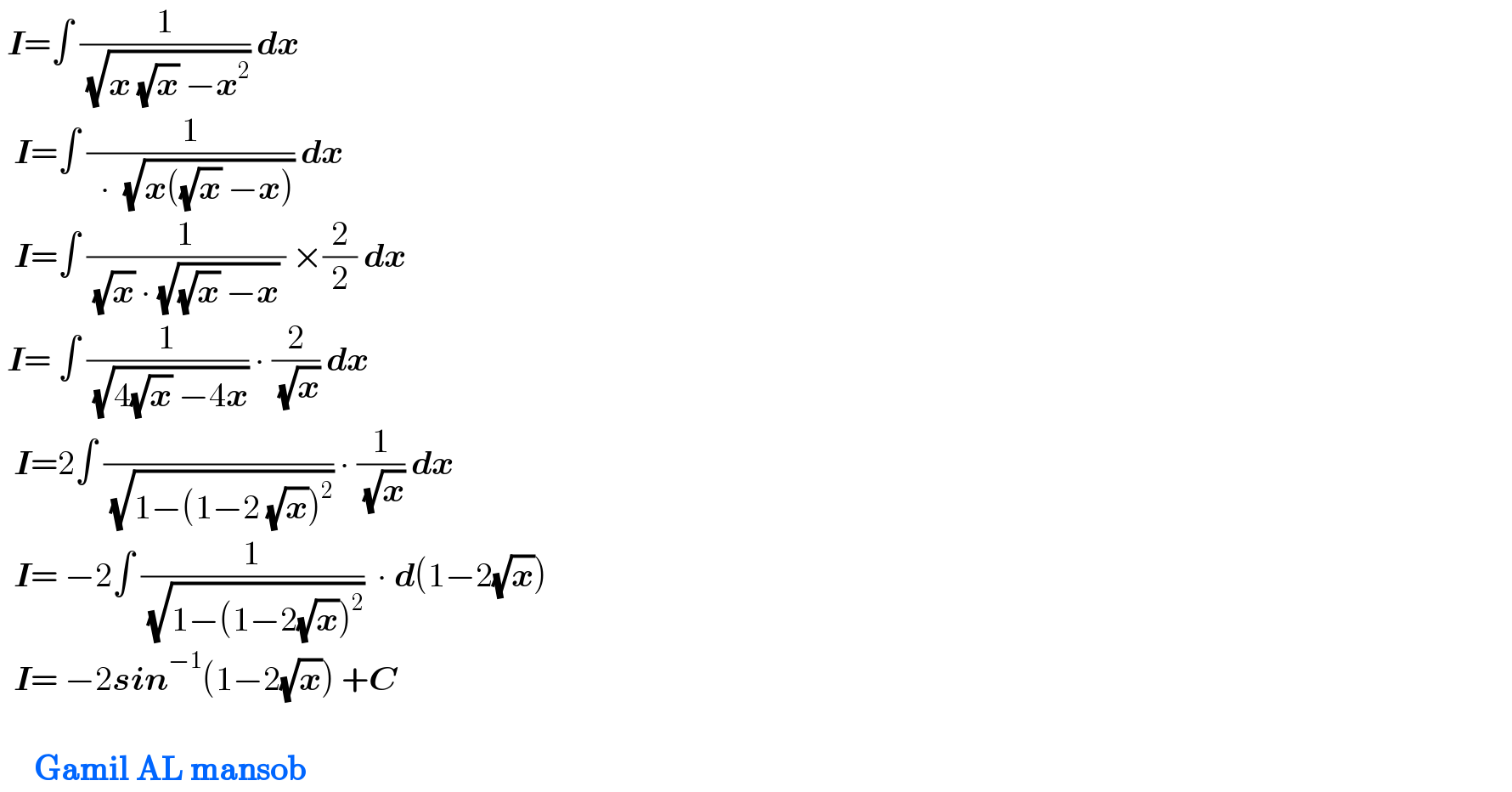
$$\:\boldsymbol{{I}}=\int\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{x}}\:\sqrt{\boldsymbol{{x}}}\:−\boldsymbol{{x}}^{\mathrm{2}} }}\:\boldsymbol{{dx}}\: \\ $$$$\:\:\boldsymbol{{I}}=\int\:\frac{\mathrm{1}}{\:\:\centerdot\:\:\sqrt{\boldsymbol{{x}}\left(\sqrt{\boldsymbol{{x}}}\:−\boldsymbol{{x}}\right)}}\:\boldsymbol{{dx}} \\ $$$$\:\:\boldsymbol{{I}}=\int\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{x}}}\:\centerdot\:\sqrt{\sqrt{\boldsymbol{{x}}}\:−\boldsymbol{{x}}}\:}\:×\frac{\mathrm{2}}{\mathrm{2}}\:\boldsymbol{{dx}} \\ $$$$\:\boldsymbol{{I}}=\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}\sqrt{\boldsymbol{{x}}}\:−\mathrm{4}\boldsymbol{{x}}}}\:\centerdot\:\frac{\mathrm{2}}{\:\sqrt{\boldsymbol{{x}}}}\:\boldsymbol{{dx}} \\ $$$$\:\:\boldsymbol{{I}}=\mathrm{2}\int\:\frac{\:}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}\:\sqrt{\boldsymbol{{x}}}\right)^{\mathrm{2}} }}\:\centerdot\:\frac{\mathrm{1}}{\:\sqrt{\boldsymbol{{x}}}}\:\boldsymbol{{dx}}\: \\ $$$$\:\:\boldsymbol{{I}}=\:−\mathrm{2}\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}\sqrt{\boldsymbol{{x}}}\right)^{\mathrm{2}} }}\:\:\centerdot\:\boldsymbol{{d}}\left(\mathrm{1}−\mathrm{2}\sqrt{\boldsymbol{{x}}}\right) \\ $$$$\:\:\boldsymbol{{I}}=\:−\mathrm{2}\boldsymbol{{sin}}^{−\mathrm{1}} \left(\mathrm{1}−\mathrm{2}\sqrt{\boldsymbol{{x}}}\right)\:+\boldsymbol{{C}} \\ $$$$\: \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{Gamil}}\:\boldsymbol{\mathrm{AL}}\:\boldsymbol{\mathrm{mansob}} \\ $$
Commented by Rasheed.Sindhi last updated on 17/Dec/22

$$ \\ $$$$\underset{\overset{\:} {\boldsymbol{\mathrm{AND}}}} {\boldsymbol{\mathrm{Question}}\:\mathrm{should}\:\mathrm{go}\:\mathrm{in}\:\mathrm{place}\:\mathrm{of}\:\boldsymbol{\mathrm{Question}}.} \\ $$$$\:\:\boldsymbol{\mathrm{Answer}}\:\mathrm{should}\:\mathrm{go}\:\mathrm{in}\:\mathrm{place}\:\mathrm{of}\:\boldsymbol{\mathrm{Answer}}. \\ $$$$ \\ $$
