Question Number 120060 by bemath last updated on 29/Oct/20
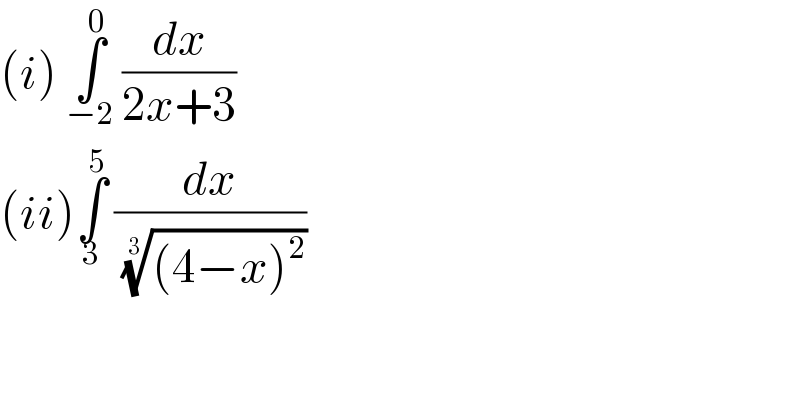
$$\left({i}\right)\:\underset{−\mathrm{2}} {\overset{\mathrm{0}} {\int}}\:\frac{{dx}}{\mathrm{2}{x}+\mathrm{3}} \\ $$$$\left({ii}\right)\underset{\mathrm{3}} {\overset{\mathrm{5}} {\int}}\:\frac{{dx}}{\:\sqrt[{\mathrm{3}}]{\left(\mathrm{4}−{x}\right)^{\mathrm{2}} }}\: \\ $$
Answered by bramlexs22 last updated on 29/Oct/20
![(ii) lim_(p→4^− ) ∫_3 ^p (dx/((4−x)^(2/3) )) + lim_(p→4^+ ) ∫_p ^5 (dx/((4−x)^(2/3) )) = lim_(p→4^− ) ∫_3 ^p (4−x)^(−2/3) dx +lim_(p→4^+ ) ∫_p ^5 (4−x)^(−2/3) dx = lim_(p→4^− ) [−3(4−x)^(1/3) ]_3 ^p + lim_(p→4^+ ) [ −3(4−x)^(1/3) ]_p ^5 = lim_(p→4^− ) [−3(4−p)^(1/3) +3 ] + lim_(p→4^+ ) [−3(−1)+3(4−p)^(1/3) ] = 6 + lim_(p→4^− ) [−3(4−p)^(1/3) ]+ lim_(p→4^+ ) [3(1−p)^(1/3) ] = 0](https://www.tinkutara.com/question/Q120062.png)
$$\left({ii}\right)\:\underset{{p}\rightarrow\mathrm{4}^{−} } {\mathrm{lim}}\:\underset{\mathrm{3}} {\overset{{p}} {\int}}\:\frac{{dx}}{\left(\mathrm{4}−{x}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} }\:+\:\underset{{p}\rightarrow\mathrm{4}^{+} } {\mathrm{lim}}\underset{{p}} {\overset{\mathrm{5}} {\int}}\:\frac{{dx}}{\left(\mathrm{4}−{x}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} } \\ $$$$=\:\underset{{p}\rightarrow\mathrm{4}^{−} } {\mathrm{lim}}\:\underset{\mathrm{3}} {\overset{{p}} {\int}}\left(\mathrm{4}−{x}\right)^{−\mathrm{2}/\mathrm{3}} \:{dx}\:+\underset{{p}\rightarrow\mathrm{4}^{+} } {\mathrm{lim}}\overset{\mathrm{5}} {\int}_{{p}} \left(\mathrm{4}−{x}\right)^{−\mathrm{2}/\mathrm{3}} \:{dx} \\ $$$$=\:\underset{{p}\rightarrow\mathrm{4}^{−} } {\mathrm{lim}}\:\left[−\mathrm{3}\left(\mathrm{4}−{x}\right)^{\mathrm{1}/\mathrm{3}} \:\right]_{\mathrm{3}} ^{{p}} \:+\:\underset{{p}\rightarrow\mathrm{4}^{+} } {\mathrm{lim}}\left[\:−\mathrm{3}\left(\mathrm{4}−{x}\right)^{\mathrm{1}/\mathrm{3}} \:\right]_{{p}} ^{\mathrm{5}} \\ $$$$=\:\underset{{p}\rightarrow\mathrm{4}^{−} } {\mathrm{lim}}\:\left[−\mathrm{3}\left(\mathrm{4}−{p}\right)^{\mathrm{1}/\mathrm{3}} +\mathrm{3}\:\right]\:+\:\underset{{p}\rightarrow\mathrm{4}^{+} } {\mathrm{lim}}\left[−\mathrm{3}\left(−\mathrm{1}\right)+\mathrm{3}\left(\mathrm{4}−{p}\right)^{\mathrm{1}/\mathrm{3}} \:\right] \\ $$$$=\:\mathrm{6}\:+\:\underset{{p}\rightarrow\mathrm{4}^{−} } {\mathrm{lim}}\:\left[−\mathrm{3}\left(\mathrm{4}−{p}\right)^{\mathrm{1}/\mathrm{3}} \:\right]+\:\underset{{p}\rightarrow\mathrm{4}^{+} } {\mathrm{lim}}\:\left[\mathrm{3}\left(\mathrm{1}−{p}\right)^{\mathrm{1}/\mathrm{3}} \:\right] \\ $$$$=\:\mathrm{0}\: \\ $$
Answered by Olaf last updated on 29/Oct/20
![(i) undefined (1/(2x+3)) is not defined for x = −(3/2) (ii) I = ∫_3 ^5 (4−x)^(−2/3) dx I = [−3(4−x)^(1/3) ]_3 ^5 = −3(−1−1) = 6](https://www.tinkutara.com/question/Q120063.png)
$$\left({i}\right) \\ $$$$\mathrm{undefined} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{x}+\mathrm{3}}\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined}\:\mathrm{for}\:{x}\:=\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$$$\left({ii}\right) \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{3}} ^{\mathrm{5}} \left(\mathrm{4}−{x}\right)^{−\mathrm{2}/\mathrm{3}} {dx} \\ $$$$\mathrm{I}\:=\:\left[−\mathrm{3}\left(\mathrm{4}−{x}\right)^{\mathrm{1}/\mathrm{3}} \right]_{\mathrm{3}} ^{\mathrm{5}} \:=\:−\mathrm{3}\left(−\mathrm{1}−\mathrm{1}\right)\:=\:\mathrm{6} \\ $$
Commented by bemath last updated on 29/Oct/20
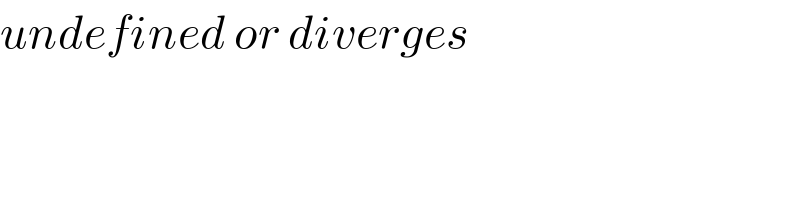
$${undefined}\:{or}\:{diverges} \\ $$
