Question Number 124277 by SOMEDAVONG last updated on 02/Dec/20
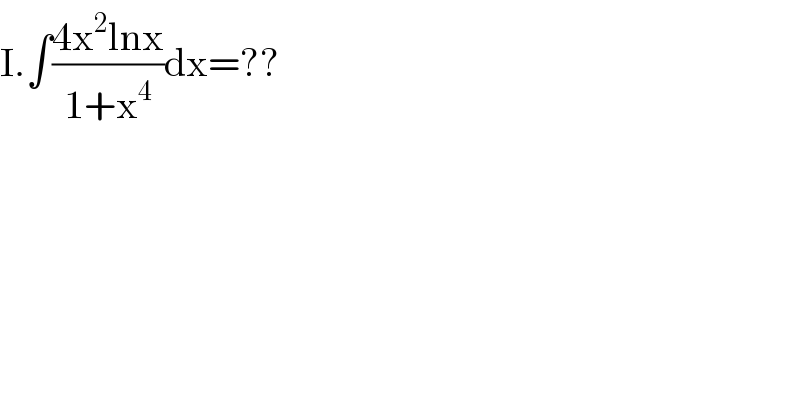
$$\mathrm{I}.\int\frac{\mathrm{4x}^{\mathrm{2}} \mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }\mathrm{dx}=?? \\ $$
Commented by MJS_new last updated on 02/Dec/20
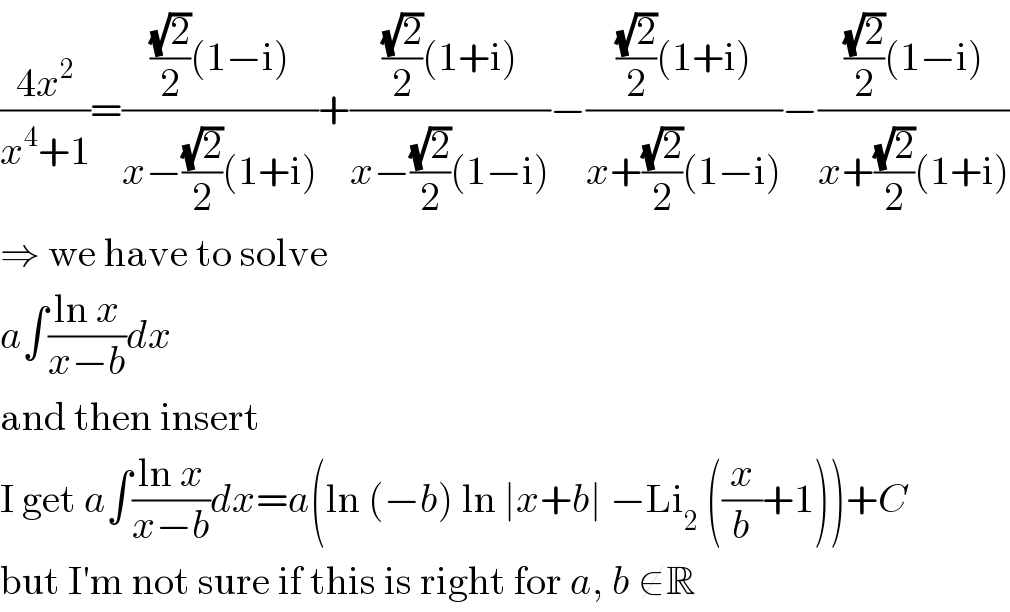
$$\frac{\mathrm{4}{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{1}}=\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{i}\right)}{{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right)}+\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right)}{{x}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{i}\right)}−\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right)}{{x}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{i}\right)}−\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{i}\right)}{{x}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{i}\right)} \\ $$$$\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve} \\ $$$${a}\int\frac{\mathrm{ln}\:{x}}{{x}−{b}}{dx} \\ $$$$\mathrm{and}\:\mathrm{then}\:\mathrm{insert} \\ $$$$\mathrm{I}\:\mathrm{get}\:{a}\int\frac{\mathrm{ln}\:{x}}{{x}−{b}}{dx}={a}\left(\mathrm{ln}\:\left(−{b}\right)\:\mathrm{ln}\:\mid{x}+{b}\mid\:−\mathrm{Li}_{\mathrm{2}} \:\left(\frac{{x}}{{b}}+\mathrm{1}\right)\right)+{C} \\ $$$$\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{if}\:\mathrm{this}\:\mathrm{is}\:\mathrm{right}\:\mathrm{for}\:{a},\:{b}\:\notin\mathbb{R} \\ $$
Commented by Dwaipayan Shikari last updated on 02/Dec/20
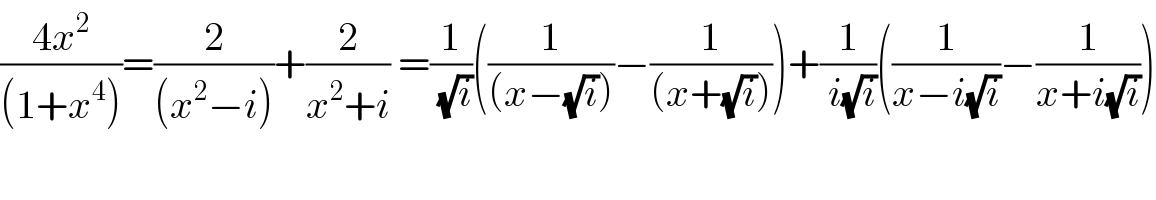
$$\frac{\mathrm{4}{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{4}} \right)}=\frac{\mathrm{2}}{\left({x}^{\mathrm{2}} −{i}\right)}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} +{i}}\:=\frac{\mathrm{1}}{\:\sqrt{{i}}}\left(\frac{\mathrm{1}}{\left({x}−\sqrt{{i}}\right)}−\frac{\mathrm{1}}{\left({x}+\sqrt{{i}}\right)}\right)+\frac{\mathrm{1}}{\:{i}\sqrt{{i}}}\left(\frac{\mathrm{1}}{{x}−{i}\sqrt{{i}}}−\frac{\mathrm{1}}{{x}+{i}\sqrt{{i}}}\right) \\ $$$$ \\ $$
