Menu Close

I-cos-2x-1-cos-2-x-dx-please-help-

Tinku Tara 0 Comments
Pin




Question Number 125711 by TITA last updated on 13/Dec/20
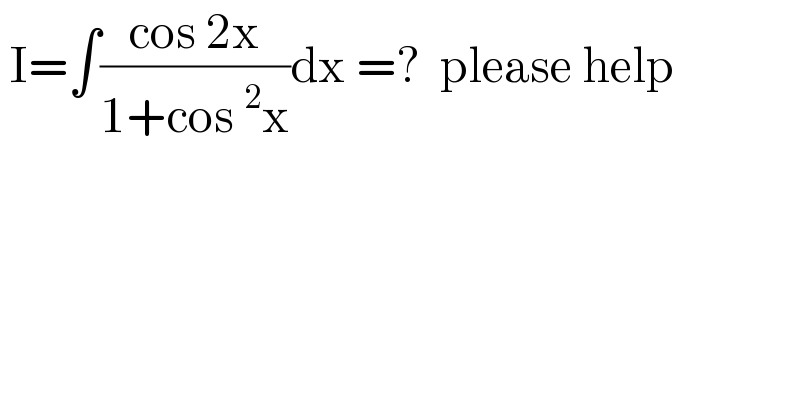
I=∫((cos 2x)/(1+cos^2 x))dx =? please help
$$\:\mathrm{I}=\int\frac{\mathrm{cos}\:\mathrm{2x}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:=?\:\:\mathrm{please}\:\mathrm{help} \\ $$$$ \\ $$
Answered by bramlexs22 last updated on 13/Dec/20
let tan (x)= t ∧ dt = (dx/(cos^2 x)) I=∫ ((2cos^2 x−1)/(1+cos^2 x)) dx = ∫ ((2((1/(1+t^2 )))−1)/(1+((1/(1+t^2 ))))) [ (1/(1+t^2 ))] dt I= ∫ (((1−t^2 )/(2+t^2 )) )((1/(1+t^2 ))) dt decomposition partial fraction ((1−t^2 )/((t^2 +2)(t^2 +1))) = ((At+B)/(t^2 +2)) + ((Ct+D)/(t^2 +1)) 1−t^2 = (At+B)(t^2 +1)+(Ct+D)(t^2 +2) t=0⇒ 1=B +2D t=i⇒ 2 = Ci +D t=−i⇒2 = −Ci+D ; gives D = 2 ∧ C=0 B = −3 t=−1⇒0 = (−A−3)(2)+2(3) −3=−A−3 ; A=0 I = ∫ −(3/(t^2 +2)) dt +∫ (2/(t^2 +1)) dt I =−(3/( (√2))) arctan ((t/( (√2))))+2 arctan (t) + c I=−(3/( (√2))) arctan (((tan x)/( (√2))))+2arctan (tan x) + c I = 2x −(3/( (√2))) arctan (((tan x)/( (√2))))+c
$${let}\:\mathrm{tan}\:\left({x}\right)=\:{t}\:\wedge\:{dt}\:=\:\frac{{dx}}{\mathrm{cos}\:^{\mathrm{2}} {x}} \\ $$$${I}=\int\:\frac{\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:=\:\int\:\frac{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)−\mathrm{1}}{\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)}\:\left[\:\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\right]\:{dt} \\ $$$${I}=\:\int\:\left(\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{2}+{t}^{\mathrm{2}} }\:\right)\left(\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)\:{dt}\:\: \\ $$$${decomposition}\:{partial}\:{fraction} \\ $$$$\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{2}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}\:=\:\frac{{At}+{B}}{{t}^{\mathrm{2}} +\mathrm{2}}\:+\:\frac{{Ct}+{D}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{1}−{t}^{\mathrm{2}} \:=\:\left({At}+{B}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)+\left({Ct}+{D}\right)\left({t}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$${t}=\mathrm{0}\Rightarrow\:\mathrm{1}={B}\:+\mathrm{2}{D} \\ $$$${t}={i}\Rightarrow\:\mathrm{2}\:=\:{Ci}\:+{D} \\ $$$${t}=−{i}\Rightarrow\mathrm{2}\:=\:−{Ci}+{D}\:;\:{gives}\:{D}\:=\:\mathrm{2}\:\wedge\:{C}=\mathrm{0} \\ $$$${B}\:=\:−\mathrm{3}\: \\ $$$${t}=−\mathrm{1}\Rightarrow\mathrm{0}\:=\:\left(−{A}−\mathrm{3}\right)\left(\mathrm{2}\right)+\mathrm{2}\left(\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{3}=−{A}−\mathrm{3}\:;\:{A}=\mathrm{0} \\ $$$${I}\:=\:\int\:−\frac{\mathrm{3}}{{t}^{\mathrm{2}} +\mathrm{2}}\:{dt}\:+\int\:\frac{\mathrm{2}}{{t}^{\mathrm{2}} +\mathrm{1}}\:{dt} \\ $$$${I}\:=−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\:\mathrm{arctan}\:\left(\frac{{t}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{2}\:\mathrm{arctan}\:\left({t}\right)\:+\:{c} \\ $$$${I}=−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\:\mathrm{arctan}\:\left(\frac{\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{2arctan}\:\left(\mathrm{tan}\:{x}\right)\:+\:{c} \\ $$$${I}\:=\:\mathrm{2}{x}\:−\frac{\mathrm{3}}{\:\sqrt{\mathrm{2}}}\:\mathrm{arctan}\:\left(\frac{\mathrm{tan}\:{x}}{\:\sqrt{\mathrm{2}}}\right)+{c}\: \\ $$$$ \\ $$
Answered by MJS_new last updated on 14/Dec/20
((cos 2x)/(1+cos^2 x))=((−1+2cos^2 x)/(1+cos^2 x))=2−(3/(1+cos^2 x)) ∫((cos 2x)/(1+cos^2 x))dx=2∫dx−3∫(dx/(1+cos^2 x)) 2∫dx=2x −3∫(dx/(1+cos^2 x))= [t=tan x → dx=cos^2 x dt] =−3∫(dt/(t^2 +2))=−((3(√2))/2)arctan (((√2)t)/2) ⇒ I=2x−((3(√2))/2)arctan (((√2)t)/2) +C
$$\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}=\frac{−\mathrm{1}+\mathrm{2cos}^{\mathrm{2}} \:{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}=\mathrm{2}−\frac{\mathrm{3}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$\int\frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}{dx}=\mathrm{2}\int{dx}−\mathrm{3}\int\frac{{dx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$$\mathrm{2}\int{dx}=\mathrm{2}{x} \\ $$$$−\mathrm{3}\int\frac{{dx}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=−\mathrm{3}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}}=−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}{t}}{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${I}=\mathrm{2}{x}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}{t}}{\mathrm{2}}\:+{C} \\ $$
Commented by bramlexs22 last updated on 14/Dec/20
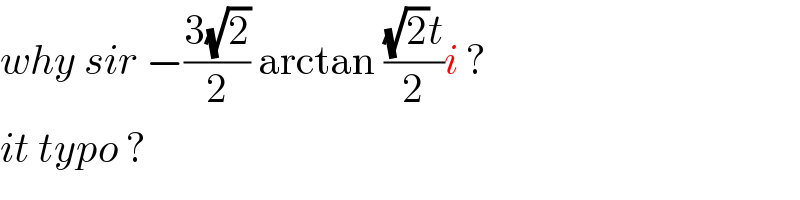
why sir −((3(√2))/2) arctan (((√2)t)/2)i ? it typo ?
$${why}\:{sir}\:−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}\:\mathrm{arctan}\:\frac{\sqrt{\mathrm{2}}{t}}{\mathrm{2}}{i}\:?\: \\ $$$${it}\:{typo}\:?\: \\ $$
Commented by MJS_new last updated on 14/Dec/20
yes, sorry
$$\mathrm{yes},\:\mathrm{sorry} \\ $$
Answered by mathmax by abdo last updated on 14/Dec/20
I =∫ ((cos(2x))/(1+cos^2 x))dx ⇒I =∫ ((cos(2x))/(1+((1+cos(2x))/2)))dx =2∫ ((cos(2x))/(3+cos(2x)))dx =_(2x=t) 2 ∫ ((cost)/(3+cost))(dt/2)=∫ ((cost)/(3+cost))dt =_(tan((t/2))=u) =∫ (((1−u^2 )/(1+u^2 ))/(3+((1−u^2 )/(1+u^2 ))))×((2du)/(1+u^2 )) =∫ ((1−u^2 )/((1+u^2 )(3+3u^2 +1−u^2 )))du =∫ ((1−u^2 )/((u^2 +1)(2u^2 +4)))du =(1/2)∫ ((1−u^2 )/((u^2 +1)(u^2 +2)))du =(1/2)∫ (1−u^2 )((1/(u^(2 ) +1))−(1/(u^(2 ) +2)))du =−(1/2)∫ ((u^2 −1)/(u^2 +1))du +(1/2)∫ ((u^2 −1)/(u^2 +2))du =−(1/2)∫ ((u^2 +1−2)/(u^2 +1))du+(1/2)∫ ((u^2 +2−3)/(u^2 +2))du =∫ (du/(u^2 +1))−(3/2)∫ (du/(u^2 +2))(→u=(√2)α) =arctan(u)−(3/2)∫ (((√2)dα)/(2(1+α^2 ))) =arctanu−((3(√2))/4)arctan((u/( (√2))))+c I=x−((3(√2))/4) arctan(((tanx)/( (√2))))+C
$$\mathrm{I}\:=\int\:\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int\:\:\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{1}+\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{2}}}\mathrm{dx}\:=\mathrm{2}\int\:\frac{\mathrm{cos}\left(\mathrm{2x}\right)}{\mathrm{3}+\mathrm{cos}\left(\mathrm{2x}\right)}\mathrm{dx} \\ $$$$=_{\mathrm{2x}=\mathrm{t}} \:\:\mathrm{2}\:\int\:\frac{\mathrm{cost}}{\mathrm{3}+\mathrm{cost}}\frac{\mathrm{dt}}{\mathrm{2}}=\int\:\:\frac{\mathrm{cost}}{\mathrm{3}+\mathrm{cost}}\mathrm{dt}\:=_{\mathrm{tan}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)=\mathrm{u}} \\ $$$$=\int\:\:\frac{\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}{\mathrm{3}+\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }}×\frac{\mathrm{2du}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\:=\int\:\:\:\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)\left(\mathrm{3}+\mathrm{3u}^{\mathrm{2}} +\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)}\mathrm{du} \\ $$$$=\int\:\:\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{2u}^{\mathrm{2}} +\mathrm{4}\right)}\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}\right)}\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}\:} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}\:} +\mathrm{2}}\right)\mathrm{du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du}\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}}\mathrm{du} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{du}+\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}−\mathrm{3}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}}\mathrm{du} \\ $$$$=\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{1}}−\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} \:+\mathrm{2}}\left(\rightarrow\mathrm{u}=\sqrt{\mathrm{2}}\alpha\right) \\ $$$$=\mathrm{arctan}\left(\mathrm{u}\right)−\frac{\mathrm{3}}{\mathrm{2}}\int\:\frac{\sqrt{\mathrm{2}}\mathrm{d}\alpha}{\mathrm{2}\left(\mathrm{1}+\alpha^{\mathrm{2}} \right)}\:=\mathrm{arctanu}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{arctan}\left(\frac{\mathrm{u}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{c} \\ $$$$\mathrm{I}=\mathrm{x}−\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\:\mathrm{arctan}\left(\frac{\mathrm{tanx}}{\:\sqrt{\mathrm{2}}}\right)+\mathrm{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *