Question Number 158591 by cortano last updated on 06/Nov/21
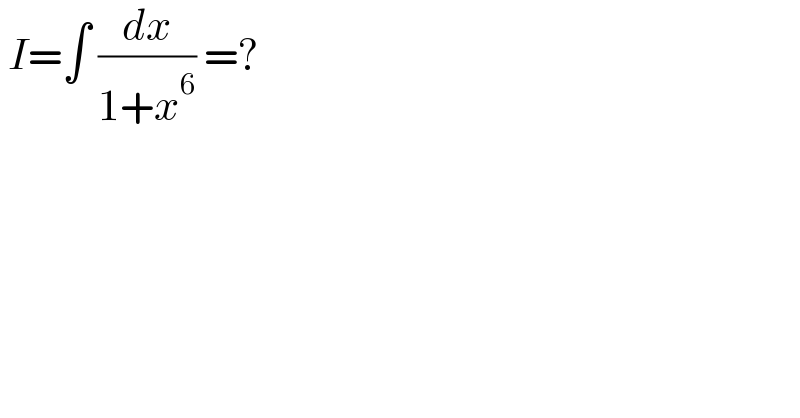
$$\:{I}=\int\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{6}} }\:=? \\ $$
Commented by tounghoungko last updated on 06/Nov/21
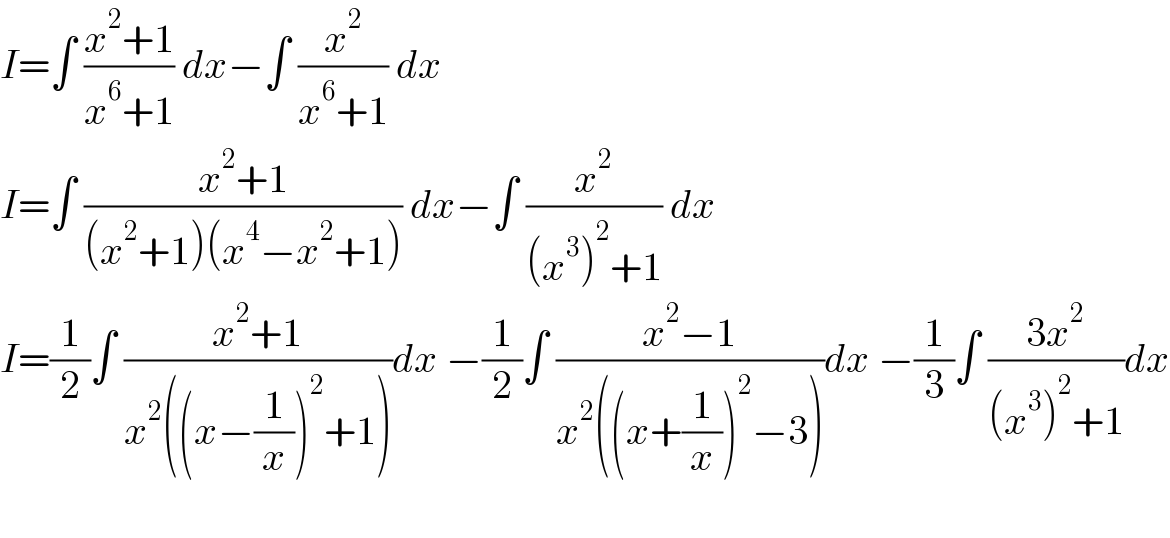
$${I}=\int\:\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{6}} +\mathrm{1}}\:{dx}−\int\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{6}} +\mathrm{1}}\:{dx} \\ $$$${I}=\int\:\frac{{x}^{\mathrm{2}} +\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)}\:{dx}−\int\:\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{1}}\:{dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}^{\mathrm{2}} \left(\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}\right)}{dx}\:−\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} \left(\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{3}\right)}{dx}\:−\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\mathrm{3}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{3}} \right)^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$ \\ $$
Commented by ilhamdiii last updated on 06/Nov/21

$${oke} \\ $$
