Menu Close

i-dx-ax-2-bx-c-3-2-

Tinku Tara 0 Comments
Pin




Question Number 58240 by salaw2000 last updated on 20/Apr/19
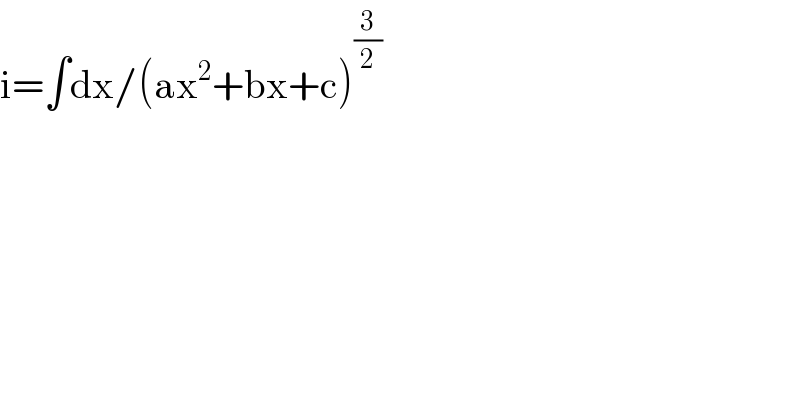
i=∫dx/(ax^2 +bx+c)^(3/2)
$$\mathrm{i}=\int\mathrm{dx}/\left(\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{c}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$
Commented by maxmathsup by imad last updated on 21/Apr/19
let I =∫ (dx/((ax^2 +bx +c)^(3/2) )) let p(x)=ax^2 +bx +c Δ =b^2 −4ac if Δ <0 ⇒non roots and p(x)=a(x^2 +2(b/(2a))x +(b^2 /(4a^2 )) +c−(b^2 /(4a^2 ))) =a{ (x+(b/(2a)))^2 +((4ac −b^2 )/(4a^2 ))} we use the changement (x+(b/(2a)))=((√(4ac−b^2 ))/(2a))sh(t) ⇒ I = ∫ (1/(a^(3/2) (((4ac−b^2 )/(4a^2 )))^(3/2) (1+sh^2 t)^(3/2) ))((√(4ac−b^2 ))/(2a)) ch(t)dt =((√(4ac−b^2 ))/(2a^(5/2) (((4ac−b^2 )/(4a^2 )))(√((4ac−b^2 )/(4a^2 ))))) ∫ (dt/(ch^3 (t))) =((2a)/(2a^(5/2) )) ((4a^2 )/(4ac−b^2 )) ∫ (dt/((((e^t +e^(−t) )/2))^3 )) =4 a^(2−(3/2)) (1/(4ac−b^2 )) ∫ (8/((e^t +e^(−t) )^3 )) dt =((32(√a))/(4ac−b^2 )) ∫ (dt/(e^(3t) +3 e^(2t) e^(−t) +3 e^t e^(−2t) +e^(−3t) )) =((32(√a))/(4ac−b^2 )) ∫ (dt/(e^(3t) +3 e^t +3 e^(−t) +e^(−3t) )) =_(e^t =u) λ ∫ (du/(u(u^3 +3u +3u^(−1) +u^(−3) ))) =λ ∫ (du/(u^4 +3u^2 +3 u^(−2) )) =λ ∫ ((u^2 du)/(u^6 +3u^4 +3)) ...be continued...
$${let}\:{I}\:=\int\:\:\frac{{dx}}{\left({ax}^{\mathrm{2}} \:+{bx}\:+{c}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:{let}\:{p}\left({x}\right)={ax}^{\mathrm{2}} \:+{bx}\:+{c} \\ $$$$\Delta\:={b}^{\mathrm{2}} −\mathrm{4}{ac}\:\:\:{if}\:\Delta\:<\mathrm{0}\:\Rightarrow{non}\:{roots}\:\:{and}\:{p}\left({x}\right)={a}\left({x}^{\mathrm{2}} \:+\mathrm{2}\frac{{b}}{\mathrm{2}{a}}{x}\:+\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\:+{c}−\frac{{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right) \\ $$$$={a}\left\{\:\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}{ac}\:−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right\}\:{we}\:{use}\:{the}\:{changement}\:\left({x}+\frac{{b}}{\mathrm{2}{a}}\right)=\frac{\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}{\mathrm{2}{a}}{sh}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\:\int\:\frac{\mathrm{1}}{{a}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}+{sh}^{\mathrm{2}} {t}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\frac{\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}{\mathrm{2}{a}}\:{ch}\left({t}\right){dt} \\ $$$$=\frac{\sqrt{\mathrm{4}{ac}−{b}^{\mathrm{2}} }}{\mathrm{2}{a}^{\frac{\mathrm{5}}{\mathrm{2}}} \:\:\:\left(\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)\sqrt{\frac{\mathrm{4}{ac}−{b}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }}}\:\int\:\:\frac{{dt}}{{ch}^{\mathrm{3}} \left({t}\right)}\:=\frac{\mathrm{2}{a}}{\mathrm{2}{a}^{\frac{\mathrm{5}}{\mathrm{2}}} }\:\frac{\mathrm{4}{a}^{\mathrm{2}} }{\mathrm{4}{ac}−{b}^{\mathrm{2}} }\:\int\:\:\:\frac{{dt}}{\left(\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}\right)^{\mathrm{3}} } \\ $$$$=\mathrm{4}\:{a}^{\mathrm{2}−\frac{\mathrm{3}}{\mathrm{2}}} \:\frac{\mathrm{1}}{\mathrm{4}{ac}−{b}^{\mathrm{2}} }\:\int\:\:\:\frac{\mathrm{8}}{\left({e}^{{t}} \:+{e}^{−{t}} \right)^{\mathrm{3}} }\:{dt}\:=\frac{\mathrm{32}\sqrt{{a}}}{\mathrm{4}{ac}−{b}^{\mathrm{2}} }\:\int\:\:\:\frac{{dt}}{{e}^{\mathrm{3}{t}} \:+\mathrm{3}\:{e}^{\mathrm{2}{t}} \:{e}^{−{t}} \:+\mathrm{3}\:{e}^{{t}} \:{e}^{−\mathrm{2}{t}} \:+{e}^{−\mathrm{3}{t}} } \\ $$$$=\frac{\mathrm{32}\sqrt{{a}}}{\mathrm{4}{ac}−{b}^{\mathrm{2}} }\:\int\:\:\frac{{dt}}{{e}^{\mathrm{3}{t}} \:+\mathrm{3}\:{e}^{{t}} \:+\mathrm{3}\:{e}^{−{t}} \:+{e}^{−\mathrm{3}{t}} }\:=_{{e}^{{t}} \:={u}} \:\:\:\lambda\:\:\int\:\:\:\:\frac{{du}}{{u}\left({u}^{\mathrm{3}} \:+\mathrm{3}{u}\:+\mathrm{3}{u}^{−\mathrm{1}} \:+{u}^{−\mathrm{3}} \right)} \\ $$$$=\lambda\:\int\:\:\:\:\frac{{du}}{{u}^{\mathrm{4}} \:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{3}\:{u}^{−\mathrm{2}} }\:=\lambda\:\int\:\:\:\:\frac{{u}^{\mathrm{2}} \:{du}}{{u}^{\mathrm{6}} \:+\mathrm{3}{u}^{\mathrm{4}} \:+\mathrm{3}}\:\:\:…{be}\:{continued}… \\ $$$$ \\ $$
Commented by salaw2000 last updated on 06/May/19
thanks sir
$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Answered by tanmay last updated on 20/Apr/19
Commented by tanmay last updated on 20/Apr/19
Commented by tanmay last updated on 20/Apr/19
(4/a^(3/2) )×(1/({(((−b)/a))^2 −((4c)/a)}))×[ln(cosecθ−cotθ)+cosθ]+c now tanθ=((√t)/((α−β)^(1/4) ))→cotθ=(((α−β)^(1/4) )/( (√t))) coesecθ=[1+(((α−β)^(1/2) )/t)]^(1/2) and cosθ=(1/([1+(t/((α−β)^(1/2) ))]^(1/2) )) (4/a^(3/2) )×(a^2 /((b^2 −4ac)))×ln(cosecθ−cotθ)+cosθ +c pls put the value of cosecθ,cotθ and cosθ finally replace t by (√(x−α))
$$\frac{\mathrm{4}}{{a}^{\frac{\mathrm{3}}{\mathrm{2}}} }×\frac{\mathrm{1}}{\left\{\left(\frac{−{b}}{{a}}\right)^{\mathrm{2}} −\frac{\mathrm{4}{c}}{{a}}\right\}}×\left[{ln}\left({cosec}\theta−{cot}\theta\right)+{cos}\theta\right]+{c} \\ $$$${now}\:{tan}\theta=\frac{\sqrt{{t}}}{\left(\alpha−\beta\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\rightarrow{cot}\theta=\frac{\left(\alpha−\beta\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }{\:\sqrt{{t}}} \\ $$$${coesec}\theta=\left[\mathrm{1}+\frac{\left(\alpha−\beta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{{t}}\right]^{\frac{\mathrm{1}}{\mathrm{2}}} {and}\:{cos}\theta=\frac{\mathrm{1}}{\left[\mathrm{1}+\frac{{t}}{\left(\alpha−\beta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }\right]^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$$$\frac{\mathrm{4}}{{a}^{\frac{\mathrm{3}}{\mathrm{2}}} }×\frac{{a}^{\mathrm{2}} }{\left({b}^{\mathrm{2}} −\mathrm{4}{ac}\right)}×{ln}\left({cosec}\theta−{cot}\theta\right)+{cos}\theta\:+{c} \\ $$$${pls}\:{put}\:{the}\:{value}\:{of}\:{cosec}\theta,{cot}\theta\:{and}\:{cos}\theta \\ $$$${finally}\:{replace}\:{t}\:{by}\:\sqrt{{x}−\alpha}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *