Question Number 165561 by LEKOUMA last updated on 03/Feb/22
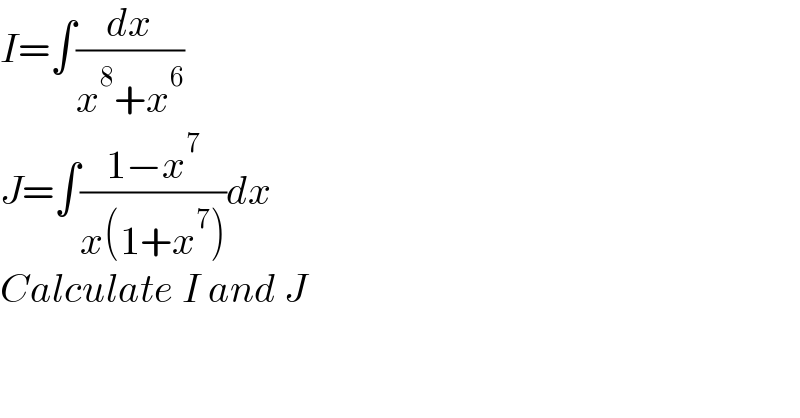
$${I}=\int\frac{{dx}}{{x}^{\mathrm{8}} +{x}^{\mathrm{6}} } \\ $$$${J}=\int\frac{\mathrm{1}−{x}^{\mathrm{7}} }{{x}\left(\mathrm{1}+{x}^{\mathrm{7}} \right)}{dx} \\ $$$${Calculate}\:{I}\:{and}\:{J} \\ $$
Answered by MJS_new last updated on 05/Feb/22
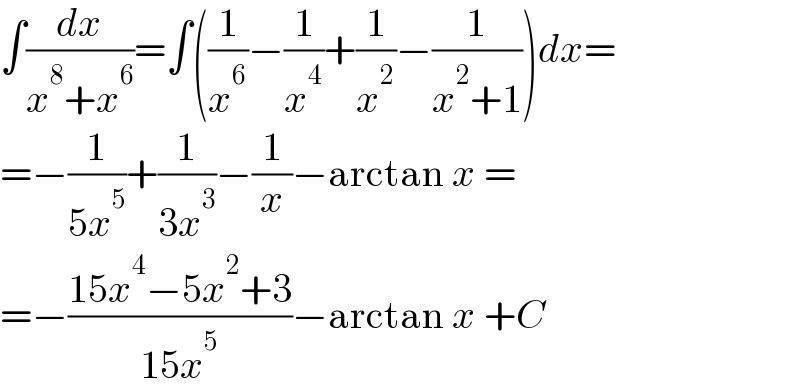
$$\int\frac{{dx}}{{x}^{\mathrm{8}} +{x}^{\mathrm{6}} }=\int\left(\frac{\mathrm{1}}{{x}^{\mathrm{6}} }−\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\right){dx}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{5}{x}^{\mathrm{5}} }+\frac{\mathrm{1}}{\mathrm{3}{x}^{\mathrm{3}} }−\frac{\mathrm{1}}{{x}}−\mathrm{arctan}\:{x}\:= \\ $$$$=−\frac{\mathrm{15}{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{15}{x}^{\mathrm{5}} }−\mathrm{arctan}\:{x}\:+{C} \\ $$
Answered by MJS_new last updated on 05/Feb/22
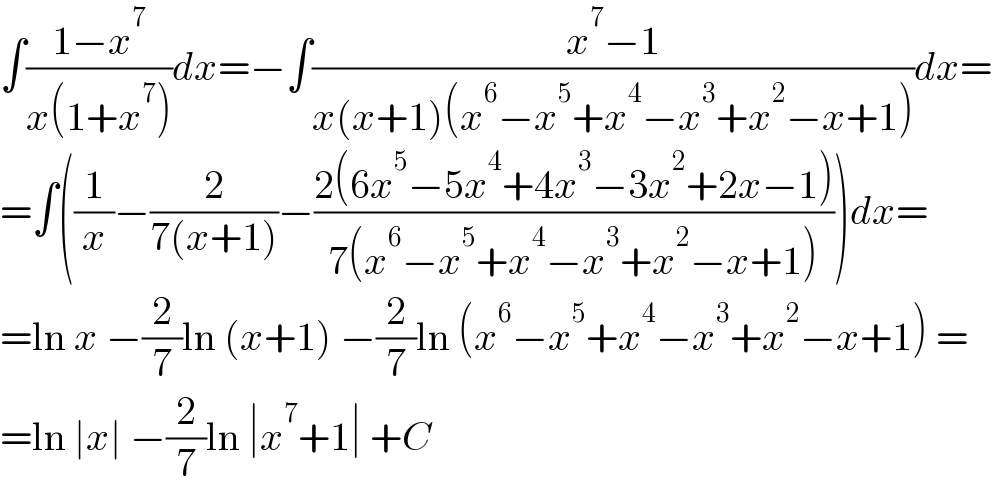
$$\int\frac{\mathrm{1}−{x}^{\mathrm{7}} }{{x}\left(\mathrm{1}+{x}^{\mathrm{7}} \right)}{dx}=−\int\frac{{x}^{\mathrm{7}} −\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{6}} −{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{dx}= \\ $$$$=\int\left(\frac{\mathrm{1}}{{x}}−\frac{\mathrm{2}}{\mathrm{7}\left({x}+\mathrm{1}\right)}−\frac{\mathrm{2}\left(\mathrm{6}{x}^{\mathrm{5}} −\mathrm{5}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{7}\left({x}^{\mathrm{6}} −{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}\right){dx}= \\ $$$$=\mathrm{ln}\:{x}\:−\frac{\mathrm{2}}{\mathrm{7}}\mathrm{ln}\:\left({x}+\mathrm{1}\right)\:−\frac{\mathrm{2}}{\mathrm{7}}\mathrm{ln}\:\left({x}^{\mathrm{6}} −{x}^{\mathrm{5}} +{x}^{\mathrm{4}} −{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:= \\ $$$$=\mathrm{ln}\:\mid{x}\mid\:−\frac{\mathrm{2}}{\mathrm{7}}\mathrm{ln}\:\mid{x}^{\mathrm{7}} +\mathrm{1}\mid\:+{C} \\ $$
