Question Number 60514 by tanmay last updated on 21/May/19
![i found some interesting basic question hence sharing... 1)if A∈[1,4] A^2 ∈ ? ←find interval 2)if A ∈ [−1,4] A^2 ∈ ? 3) y=(1/(A )) and A∈ [1,4] y∈ ? 4)y=(1/(∣A∣)) A∈[−1,4] y∈ ?](https://www.tinkutara.com/question/Q60514.png)
$${i}\:{found}\:{some}\:{interesting}\:{basic}\:{question} \\ $$$${hence}\:{sharing}… \\ $$$$\left.\mathrm{1}\right){if}\:{A}\in\left[\mathrm{1},\mathrm{4}\right]\:\:{A}^{\mathrm{2}} \:\in\:\:?\:\leftarrow{find}\:{interval}\: \\ $$$$\left.\mathrm{2}\right){if}\:{A}\:\in\:\left[−\mathrm{1},\mathrm{4}\right]\:\:{A}^{\mathrm{2}} \:\in\:? \\ $$$$\left.\mathrm{3}\right)\:{y}=\frac{\mathrm{1}}{{A}\:\:}\:\:{and}\:{A}\in\:\:\:\:\left[\mathrm{1},\mathrm{4}\right]\:\:{y}\in\:? \\ $$$$\left.\mathrm{4}\right){y}=\frac{\mathrm{1}}{\mid{A}\mid}\:\:{A}\in\left[−\mathrm{1},\mathrm{4}\right]\:\:\:{y}\in\:? \\ $$
Commented by kaivan.ahmadi last updated on 22/May/19
![1. A^2 ∈[1,16] 2. A^2 ∈[0,16] 3. 1≤A≤4⇒1≥(1/A)≥(1/4)⇒(1/4)≤y≤1 4. if A≠0 −1≤A<0⇒0<∣A∣≤1⇒(1/(∣A∣))≥1 0<A≤4⇒(1/(∣A∣))≥(1/4) ⇒y≥(1/4)](https://www.tinkutara.com/question/Q60556.png)
$$\mathrm{1}.\:\:{A}^{\mathrm{2}} \in\left[\mathrm{1},\mathrm{16}\right] \\ $$$$\mathrm{2}.\:\:{A}^{\mathrm{2}} \in\left[\mathrm{0},\mathrm{16}\right] \\ $$$$\mathrm{3}.\:\:\mathrm{1}\leqslant{A}\leqslant\mathrm{4}\Rightarrow\mathrm{1}\geqslant\frac{\mathrm{1}}{{A}}\geqslant\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\frac{\mathrm{1}}{\mathrm{4}}\leqslant{y}\leqslant\mathrm{1} \\ $$$$\mathrm{4}.\:\:{if}\:{A}\neq\mathrm{0} \\ $$$$−\mathrm{1}\leqslant{A}<\mathrm{0}\Rightarrow\mathrm{0}<\mid{A}\mid\leqslant\mathrm{1}\Rightarrow\frac{\mathrm{1}}{\mid{A}\mid}\geqslant\mathrm{1} \\ $$$$\mathrm{0}<{A}\leqslant\mathrm{4}\Rightarrow\frac{\mathrm{1}}{\mid{A}\mid}\geqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow{y}\geqslant\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Commented by tanmay last updated on 22/May/19
![1)let A=x and y=x^2 A∈[1,4] so A^2 ∈[1,16] 2)A∈[−1,4] from graph y=x^2 minimum value of x^2 =0 so A^2 ∈[0,16]](https://www.tinkutara.com/question/Q60560.png)
$$\left.\mathrm{1}\right){let}\:{A}={x}\:\:{and}\:\:{y}={x}^{\mathrm{2}} \\ $$$${A}\in\left[\mathrm{1},\mathrm{4}\right]\:\:\:{so}\:{A}^{\mathrm{2}} \in\left[\mathrm{1},\mathrm{16}\right] \\ $$$$\left.\mathrm{2}\right){A}\in\left[−\mathrm{1},\mathrm{4}\right]\:\:{from}\:{graph}\:{y}={x}^{\mathrm{2}} \: \\ $$$${minimum}\:{value}\:{of}\:{x}^{\mathrm{2}} =\mathrm{0} \\ $$$${so}\:{A}^{\mathrm{2}} \in\left[\mathrm{0},\mathrm{16}\right] \\ $$
Commented by tanmay last updated on 22/May/19
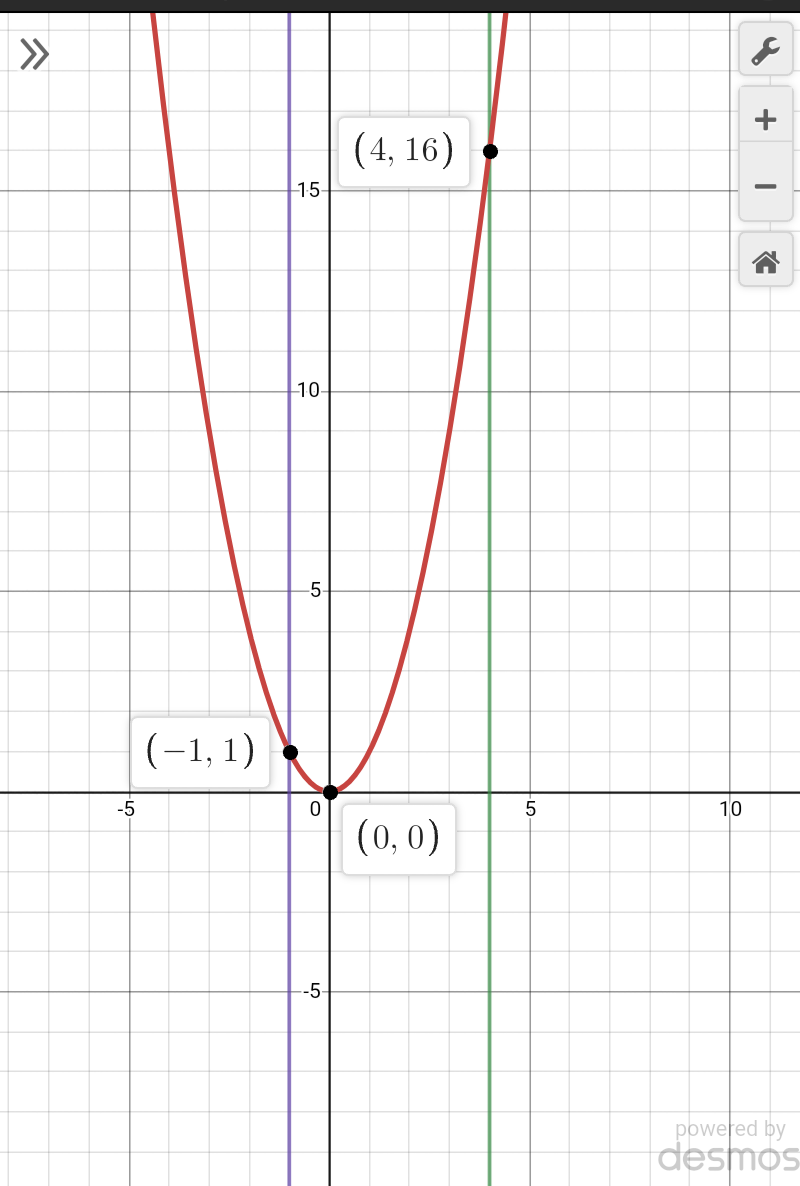
Commented by tanmay last updated on 22/May/19
![3)let x=A and y=(1/A) A∈[1,4] (1/A)∈[0.25,1]](https://www.tinkutara.com/question/Q60562.png)
$$\left.\mathrm{3}\right){let}\:{x}={A}\:\:{and}\:{y}=\frac{\mathrm{1}}{{A}} \\ $$$${A}\in\left[\mathrm{1},\mathrm{4}\right]\:\:\frac{\mathrm{1}}{{A}}\in\left[\mathrm{0}.\mathrm{25},\mathrm{1}\right] \\ $$$$ \\ $$
Commented by tanmay last updated on 22/May/19
$${thank}\:{you}\:{sir} \\ $$
Answered by tanmay last updated on 22/May/19
![4) A=x y=(1/(∣x∣)) when x=−1 y=(1/(∣−1∣))=1 when x=4 y=(1/4) A∈[−1,4] (1/([A]))∈ [1,∞) ∩ [(1/4),∞)](https://www.tinkutara.com/question/Q60564.png)
$$\left.\mathrm{4}\right)\:{A}={x}\:\:\:{y}=\frac{\mathrm{1}}{\mid{x}\mid} \\ $$$${when}\:{x}=−\mathrm{1}\:\:{y}=\frac{\mathrm{1}}{\mid−\mathrm{1}\mid}=\mathrm{1} \\ $$$${when}\:{x}=\mathrm{4}\:\:{y}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${A}\in\left[−\mathrm{1},\mathrm{4}\right] \\ $$$$\frac{\mathrm{1}}{\left[{A}\right]}\in\:\left[\mathrm{1},\infty\right)\:\cap\:\left[\frac{\mathrm{1}}{\mathrm{4}},\infty\right) \\ $$
Commented by tanmay last updated on 22/May/19
Commented by MJS last updated on 22/May/19
$$\left[\mathrm{1},\:\infty\right)\cap\left[\frac{\mathrm{1}}{\mathrm{4}},\:\infty\right)\:=\:\left[\mathrm{1},\:\infty\right) \\ $$$$\mathrm{so}\:\mathrm{your}\:\mathrm{conclusion}\:\mathrm{is}\:\mathrm{wrong}.\:\mathrm{the}\:\mathrm{path}\:\mathrm{is}\:\mathrm{ok}. \\ $$$$\frac{\mathrm{1}}{\mid{A}\mid}\in\left[\frac{\mathrm{1}}{\mathrm{4}},\:\infty\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{right}\:\mathrm{answer} \\ $$
Commented by tanmay last updated on 22/May/19
$${thank}\:{you}\:{sir}… \\ $$