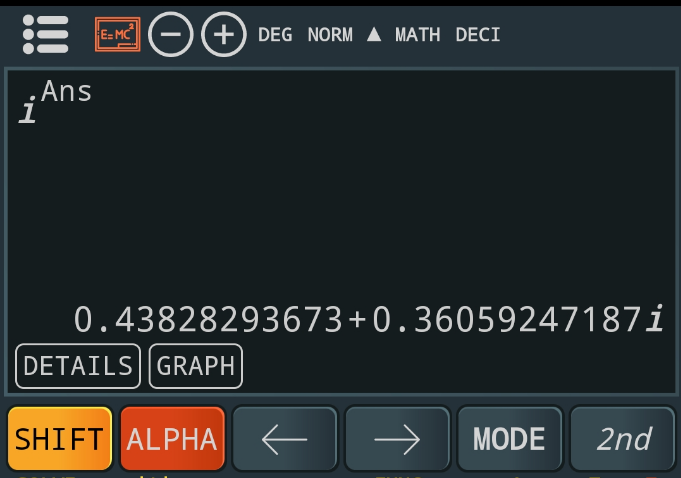
Question Number 101303 by Dwaipayan Shikari last updated on 01/Jul/20

$${i}^{{i}^{{i}.\infty} } =? \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jul/20
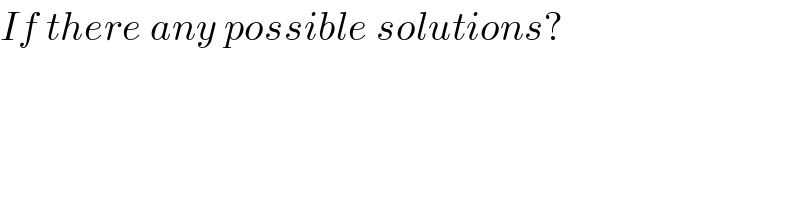
$${If}\:{there}\:{any}\:{possible}\:{solutions}? \\ $$
Answered by mr W last updated on 01/Jul/20
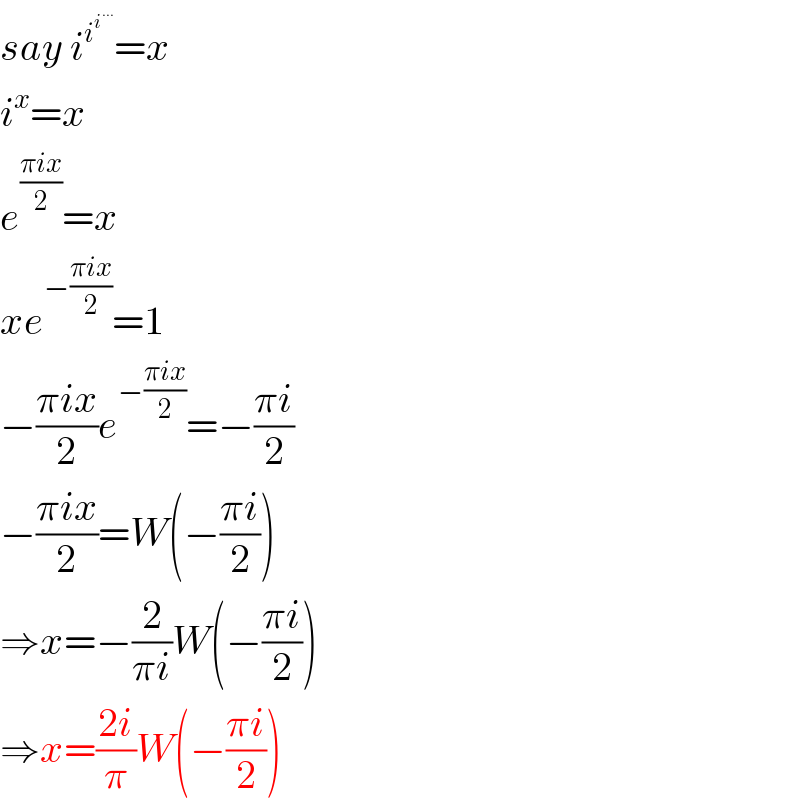
$${say}\:{i}^{{i}^{{i}^{…} } } ={x} \\ $$$${i}^{{x}} ={x} \\ $$$${e}^{\frac{\pi{ix}}{\mathrm{2}}} ={x} \\ $$$${xe}^{−\frac{\pi{ix}}{\mathrm{2}}} =\mathrm{1} \\ $$$$−\frac{\pi{ix}}{\mathrm{2}}{e}^{−\frac{\pi{ix}}{\mathrm{2}}} =−\frac{\pi{i}}{\mathrm{2}} \\ $$$$−\frac{\pi{ix}}{\mathrm{2}}={W}\left(−\frac{\pi{i}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{2}}{\pi{i}}{W}\left(−\frac{\pi{i}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}{i}}{\pi}{W}\left(−\frac{\pi{i}}{\mathrm{2}}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 01/Jul/20

$${Thanking}\:{you} \\ $$
Commented by mr W last updated on 01/Jul/20