Question Number 100584 by Dwaipayan Shikari last updated on 27/Jun/20

$$\int{i}^{{i}^{{i}……\infty} } {dx} \\ $$
Answered by MJS last updated on 27/Jun/20
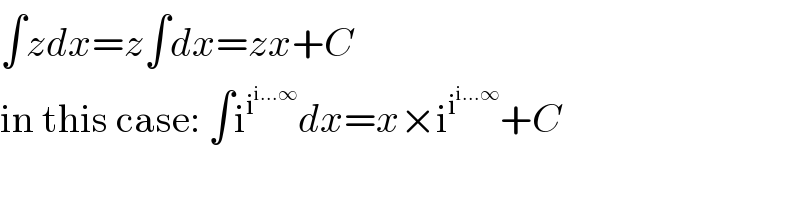
$$\int{zdx}={z}\int{dx}={zx}+{C} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}:\:\int\mathrm{i}^{\mathrm{i}^{\mathrm{i}…\infty} } {dx}={x}×\mathrm{i}^{\mathrm{i}^{\mathrm{i}…\infty} } +{C} \\ $$
Commented by Dwaipayan Shikari last updated on 27/Jun/20
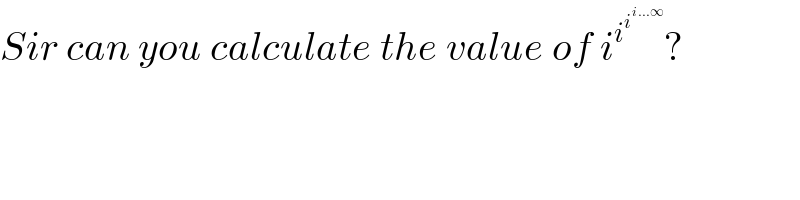
$${Sir}\:{can}\:{you}\:{calculate}\:{the}\:{value}\:{of}\:{i}^{{i}^{{i}^{{i}…\infty} } } ? \\ $$
Commented by Dwaipayan Shikari last updated on 27/Jun/20
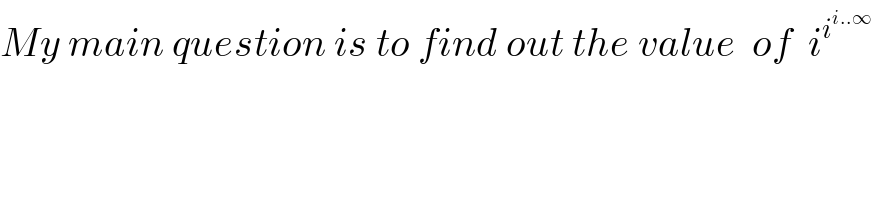
$${My}\:{main}\:{question}\:{is}\:{to}\:{find}\:{out}\:{the}\:{value}\:\:{of}\:\:{i}^{{i}^{{i}..\infty} } \\ $$
Commented by MJS last updated on 27/Jun/20

$$\mathrm{usually} \\ $$$${x}^{{x}^{{x}…} } ={y} \\ $$$$\Rightarrow \\ $$$${x}^{{y}} ={y} \\ $$$${y}\:\mathrm{ln}\:{x}\:=\mathrm{ln}\:{y} \\ $$$$−\frac{\mathrm{ln}\:{y}}{{y}}=−\mathrm{ln}\:{x} \\ $$$${y}=\mathrm{e}^{−{t}} \\ $$$$\mathrm{e}^{{t}} {t}=−\mathrm{ln}\:{x} \\ $$$$\mathrm{we}\:\mathrm{need}\:\mathrm{the}\:\mathrm{Lambert}\:\mathrm{W}\:\mathrm{function},\:\mathrm{I}\:\mathrm{don}'\mathrm{t} \\ $$$$\mathrm{know}\:\mathrm{if}\:\mathrm{there}\:\mathrm{are}\:\mathrm{solutions}\:\mathrm{for}\:{x}\notin\mathbb{R} \\ $$
Commented by MJS last updated on 27/Jun/20
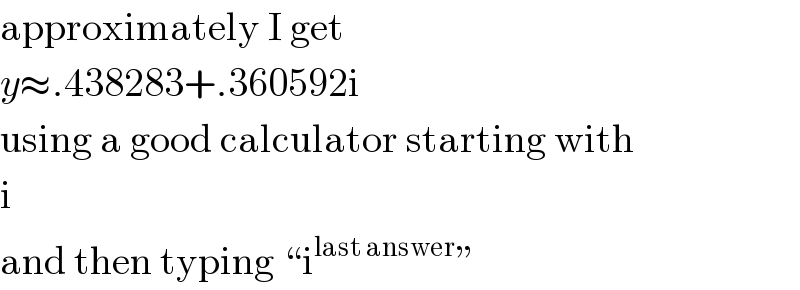
$$\mathrm{approximately}\:\mathrm{I}\:\mathrm{get} \\ $$$${y}\approx.\mathrm{438283}+.\mathrm{360592i} \\ $$$$\mathrm{using}\:\mathrm{a}\:\mathrm{good}\:\mathrm{calculator}\:\mathrm{starting}\:\mathrm{with} \\ $$$$\mathrm{i} \\ $$$$\mathrm{and}\:\mathrm{then}\:\mathrm{typing}\:“\mathrm{i}^{\mathrm{last}\:\mathrm{answer}} '' \\ $$
Commented by Dwaipayan Shikari last updated on 27/Jun/20

$${Thanking}\:{you}\:{for}\:{interacting} \\ $$
