Menu Close

i-L-lim-x-0-1-x-1-x-e-1-x-ii-L-lim-x-x-e-x-x-x-1-x-

Tinku Tara 0 Comments
Pin




Question Number 107745 by ajfour last updated on 12/Aug/20
(i) L=lim_(x→0) [(((1+x)^(1/x) )/e)]^(1/x) = ? (ii) L=lim_(x→∞) [(x/e)−x((x/(x+1)))^x ] = ?
$$\left({i}\right)\:\:\:{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{1}/{x}} }{{e}}\right]^{\mathrm{1}/{x}} \:\:=\:? \\ $$$$\left({ii}\right)\:\:{L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left[\frac{{x}}{{e}}−{x}\left(\frac{{x}}{{x}+\mathrm{1}}\right)^{{x}} \right]\:=\:? \\ $$
Commented by ajfour last updated on 12/Aug/20
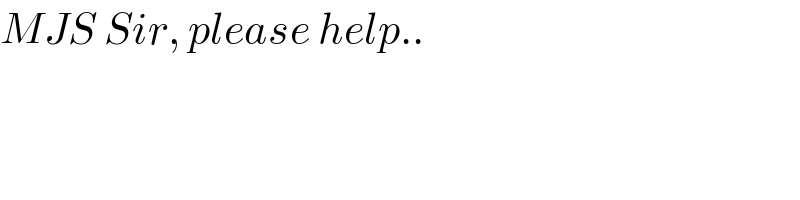
MJS Sir, please help..
$${MJS}\:{Sir},\:{please}\:{help}.. \\ $$
Commented by bemath last updated on 13/Aug/20
Commented by bobhans last updated on 13/Aug/20
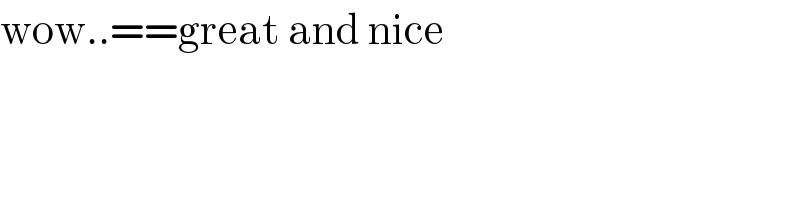
wow..==great and nice
$$\mathrm{wow}..==\mathrm{great}\:\mathrm{and}\:\mathrm{nice} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Aug/20
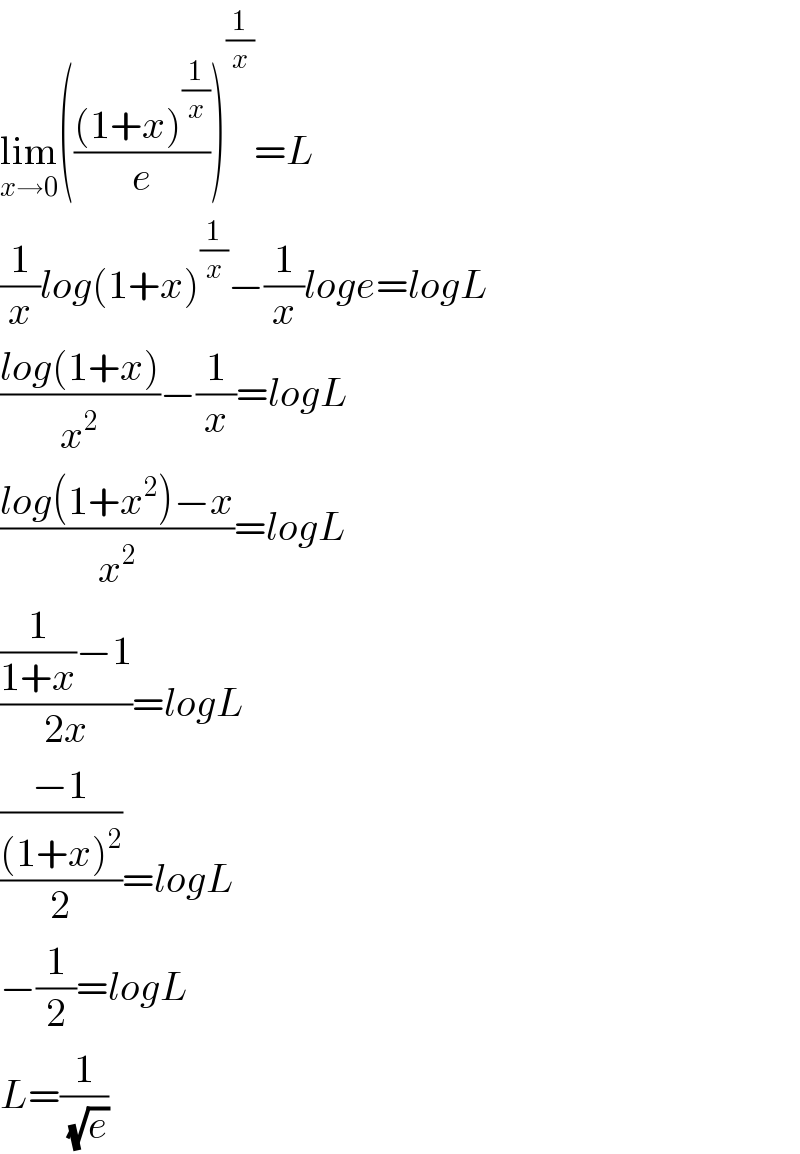
lim_(x→0) ((((1+x)^(1/x) )/e))^(1/x) =L (1/x)log(1+x)^(1/x) −(1/x)loge=logL ((log(1+x))/x^2 )−(1/x)=logL ((log(1+x^2 )−x)/x^2 )=logL (((1/(1+x))−1)/(2x))=logL (((−1)/((1+x)^2 ))/2)=logL −(1/2)=logL L=(1/( (√e)))
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} }{{e}}\right)^{\frac{\mathrm{1}}{{x}}} ={L} \\ $$$$\frac{\mathrm{1}}{{x}}{log}\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} −\frac{\mathrm{1}}{{x}}{loge}={logL} \\ $$$$\frac{{log}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}={logL} \\ $$$$\frac{{log}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)−{x}}{{x}^{\mathrm{2}} }={logL} \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{1}+{x}}−\mathrm{1}}{\mathrm{2}{x}}={logL} \\ $$$$\frac{\frac{−\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }}{\mathrm{2}}={logL} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}={logL} \\ $$$${L}=\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
Commented by ajfour last updated on 12/Aug/20
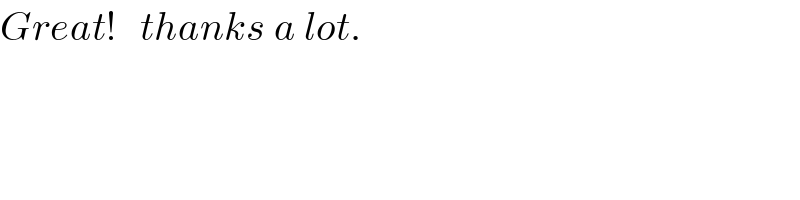
Great! thanks a lot.
$${Great}!\:\:\:{thanks}\:{a}\:{lot}. \\ $$
Commented by Dwaipayan Shikari last updated on 12/Aug/20
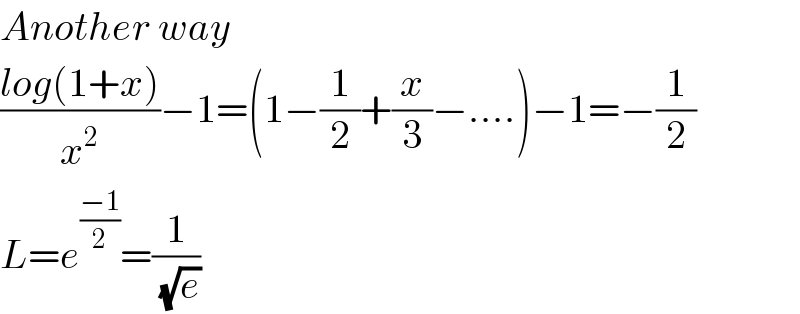
Another way ((log(1+x))/x^2 )−1=(1−(1/2)+(x/3)−....)−1=−(1/2) L=e^((−1)/2) =(1/( (√e)))
$${Another}\:{way} \\ $$$$\frac{{log}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} }−\mathrm{1}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{{x}}{\mathrm{3}}−….\right)−\mathrm{1}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${L}={e}^{\frac{−\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\:\sqrt{{e}}} \\ $$
Commented by bemath last updated on 13/Aug/20
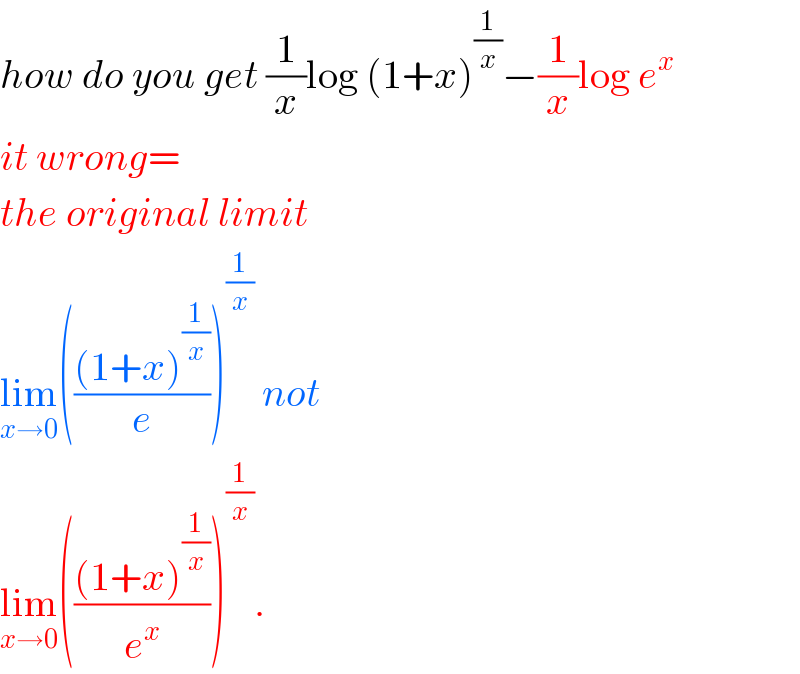
how do you get (1/x)log (1+x)^(1/x) −(1/x)log e^x it wrong= the original limit lim_(x→0) ((((1+x)^(1/x) )/e))^(1/x) not lim_(x→0) ((((1+x)^(1/x) )/e^x ))^(1/x) .
$${how}\:{do}\:{you}\:{get}\:\frac{\mathrm{1}}{{x}}\mathrm{log}\:\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} −\frac{\mathrm{1}}{{x}}\mathrm{log}\:{e}^{{x}} \\ $$$${it}\:{wrong}= \\ $$$${the}\:{original}\:{limit}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} }{{e}}\right)^{\frac{\mathrm{1}}{{x}}} \:{not}\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{{x}}} }{{e}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} . \\ $$
Answered by mathmax by abdo last updated on 12/Aug/20
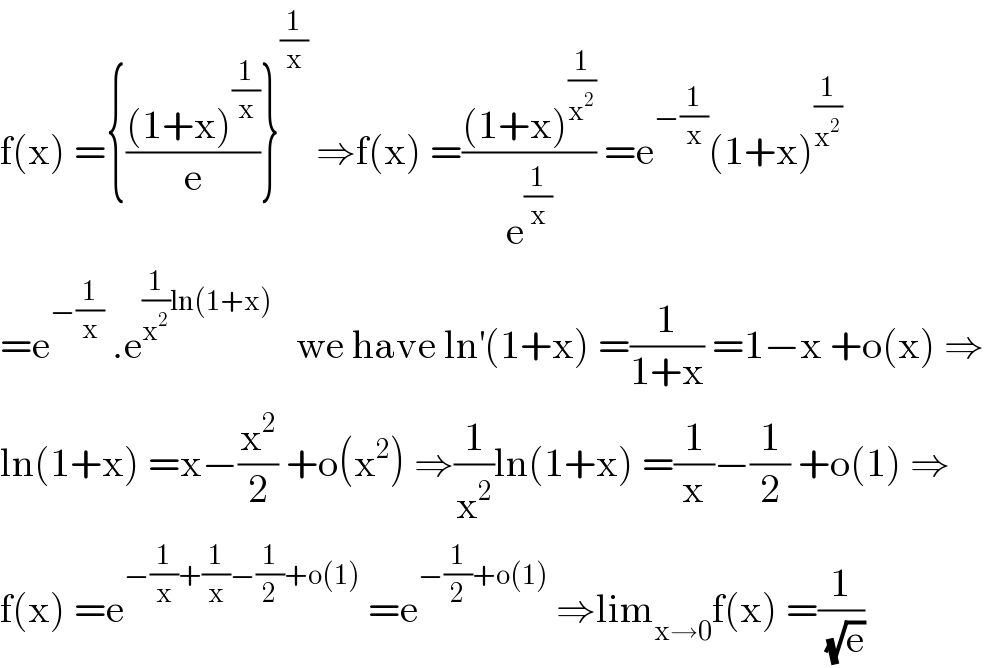
f(x) ={(((1+x)^(1/x) )/e)}^(1/x) ⇒f(x) =(((1+x)^(1/x^2 ) )/e^(1/x) ) =e^(−(1/x)) (1+x)^(1/x^2 ) =e^(−(1/x)) .e^((1/x^2 )ln(1+x)) we have ln^′ (1+x) =(1/(1+x)) =1−x +o(x) ⇒ ln(1+x) =x−(x^2 /2) +o(x^2 ) ⇒(1/x^2 )ln(1+x) =(1/x)−(1/2) +o(1) ⇒ f(x) =e^(−(1/x)+(1/x)−(1/2)+o(1)) =e^(−(1/2)+o(1)) ⇒lim_(x→0) f(x) =(1/( (√e)))
$$\mathrm{f}\left(\mathrm{x}\right)\:=\left\{\frac{\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} }{\mathrm{e}}\right\}^{\frac{\mathrm{1}}{\mathrm{x}}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} }{\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}}} }\:=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \left(\mathrm{1}+\mathrm{x}\right)^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }} \\ $$$$=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}} \:.\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)} \:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:=\mathrm{1}−\mathrm{x}\:+\mathrm{o}\left(\mathrm{x}\right)\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:=\mathrm{x}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{o}\left(\mathrm{x}^{\mathrm{2}} \right)\:\Rightarrow\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{o}\left(\mathrm{1}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{x}}+\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{o}\left(\mathrm{1}\right)} \:=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{o}\left(\mathrm{1}\right)} \:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{e}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *