Question Number 120067 by bramlexs22 last updated on 29/Oct/20

$$\left({i}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} \:\mathrm{sin}\:\left(\mathrm{1}/{x}\right)}{\mathrm{tan}\:{x}} \\ $$$$\left({ii}\right)\:{Without}\:{L}'{Hopital}\:{rule} \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}−{x}\mathrm{sin}\:{x}}{\mathrm{2}−\mathrm{2cos}\:{x}−\mathrm{sin}\:^{\mathrm{2}} {x}} \\ $$
Answered by Olaf last updated on 29/Oct/20
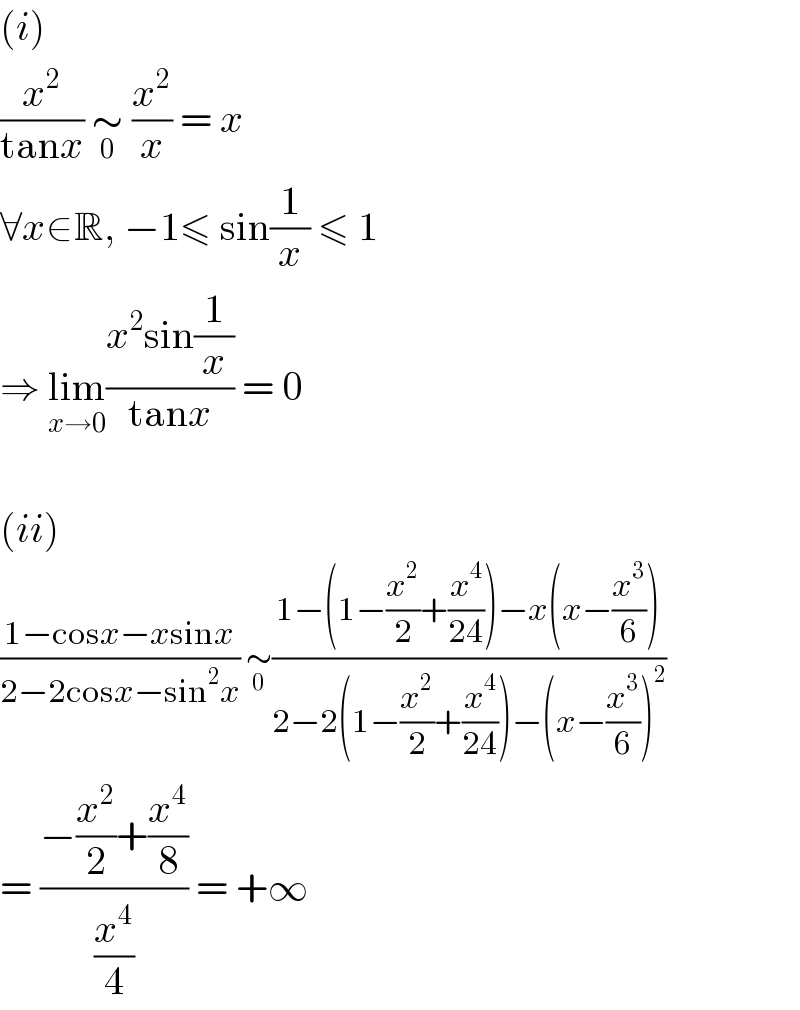
$$\left({i}\right) \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{tan}{x}}\:\underset{\mathrm{0}} {\sim}\:\frac{{x}^{\mathrm{2}} }{{x}}\:=\:{x} \\ $$$$\forall{x}\in\mathbb{R},\:−\mathrm{1}\leqslant\:\mathrm{sin}\frac{\mathrm{1}}{{x}}\:\leqslant\:\mathrm{1} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} \mathrm{sin}\frac{\mathrm{1}}{{x}}}{\mathrm{tan}{x}}\:=\:\mathrm{0} \\ $$$$ \\ $$$$\left({ii}\right) \\ $$$$\frac{\mathrm{1}−\mathrm{cos}{x}−{x}\mathrm{sin}{x}}{\mathrm{2}−\mathrm{2cos}{x}−\mathrm{sin}^{\mathrm{2}} {x}}\:\underset{\mathrm{0}} {\sim}\frac{\mathrm{1}−\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{24}}\right)−{x}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)}{\mathrm{2}−\mathrm{2}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{24}}\right)−\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\right)^{\mathrm{2}} } \\ $$$$=\:\frac{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{{x}^{\mathrm{4}} }{\mathrm{8}}}{\frac{{x}^{\mathrm{4}} }{\mathrm{4}}}\:=\:+\infty \\ $$
Answered by Bird last updated on 29/Oct/20
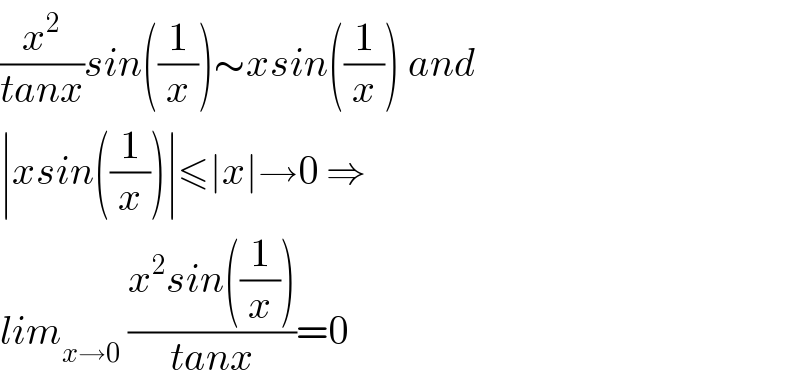
$$\frac{{x}^{\mathrm{2}} }{{tanx}}{sin}\left(\frac{\mathrm{1}}{{x}}\right)\sim{xsin}\left(\frac{\mathrm{1}}{{x}}\right)\:{and} \\ $$$$\mid{xsin}\left(\frac{\mathrm{1}}{{x}}\right)\mid\leqslant\mid{x}\mid\rightarrow\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{x}^{\mathrm{2}} {sin}\left(\frac{\mathrm{1}}{{x}}\right)}{{tanx}}=\mathrm{0} \\ $$
