Question Number 184349 by alcohol last updated on 05/Jan/23
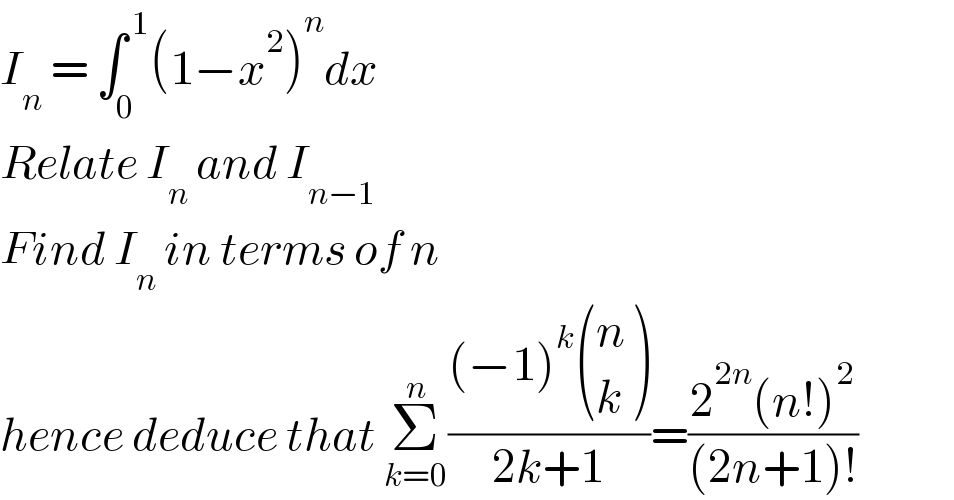
$${I}_{{n}} \:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx} \\ $$$${Relate}\:{I}_{{n}} \:{and}\:{I}_{{n}−\mathrm{1}} \\ $$$${Find}\:{I}_{{n}} \:{in}\:{terms}\:{of}\:{n} \\ $$$${hence}\:{deduce}\:{that}\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}}{\mathrm{2}{k}+\mathrm{1}}=\frac{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$
Answered by mr W last updated on 05/Jan/23
![I_n =∫_0 ^1 (1−x^2 )^n dx =[x(1−x^2 )^n ]_0 ^1 +2n∫_0 ^1 x^2 (1−x^2 )^(n−1) dx =2n∫_0 ^1 (1+x^2 −1)(1−x^2 )^(n−1) dx =2n∫_0 ^1 (1−x^2 )^(n−1) dx−2n∫_0 ^1 (1−x^2 )^n dx =2nI_(n−1) −2nI_n ⇒I_n =((2n)/(2n+1))I_(n−1) I_n =((2n)/(2n+1))×((2n−2)/(2n−1))×...×(2/3)×I_0 I_0 =∫_0 ^1 dx=1 ⇒I_n =(((2n)!!)/((2n+1)!!))=(([(2n)!!]^2 )/((2n+1)!))=(([2^n n!]^2 )/((2n+1)!))=((2^(2n) (n!)^2 )/((2n+1)!)) on the other side: I_n =∫_0 ^1 (1−x^2 )^n dx =∫_0 ^1 [Σ_(k=0) ^n ((n),(k) )(−x^2 )^k ]dx =Σ_(k=0) ^n (−1)^k ((n),(k) )[∫_0 ^1 x^(2k) dx] =Σ_(k=0) ^n (−1)^k ((n),(k) )[(x^(2k+1) /(2k+1))]_0 ^1 =Σ_(k=0) ^n (((−1)^k )/(2k+1)) ((n),(k) ) ⇒Σ_(k=0) ^n (((−1)^k )/(2k+1)) ((n),(k) ) =((2^(2n) (n!)^2 )/((2n+1)!))](https://www.tinkutara.com/question/Q184353.png)
$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx} \\ $$$$\:\:=\left[{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} \right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{2}{n}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx} \\ $$$$\:\:=\mathrm{2}{n}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx} \\ $$$$\:\:=\mathrm{2}{n}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}−\mathrm{1}} {dx}−\mathrm{2}{n}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx} \\ $$$$\:\:=\mathrm{2}{nI}_{{n}−\mathrm{1}} −\mathrm{2}{nI}_{{n}} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}}{I}_{{n}−\mathrm{1}} \\ $$$${I}_{{n}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{1}}×\frac{\mathrm{2}{n}−\mathrm{2}}{\mathrm{2}{n}−\mathrm{1}}×…×\frac{\mathrm{2}}{\mathrm{3}}×{I}_{\mathrm{0}} \\ $$$${I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} {dx}=\mathrm{1} \\ $$$$\Rightarrow{I}_{{n}} =\frac{\left(\mathrm{2}{n}\right)!!}{\left(\mathrm{2}{n}+\mathrm{1}\right)!!}=\frac{\left[\left(\mathrm{2}{n}\right)!!\right]^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}=\frac{\left[\mathrm{2}^{{n}} {n}!\right]^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}=\frac{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$ \\ $$$${on}\:{the}\:{other}\:{side}: \\ $$$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{{n}} {dx} \\ $$$$\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left[\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\left(−{x}^{\mathrm{2}} \right)^{{k}} \right]{dx} \\ $$$$\:\:=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\left[\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{k}} {dx}\right] \\ $$$$\:\:=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\left[\frac{{x}^{\mathrm{2}{k}+\mathrm{1}} }{\mathrm{2}{k}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}{k}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:=\frac{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$
