I-n-0-ln-x-cosh-n-x-dx-is-there-a-simpler-way-to-calculat-those-values-

Question Number 103397 by frc2crc last updated on 14/Jul/20

I (n) = \int_{0}^{\infty} \frac{\ln x}{\cosh^{n} x} d x

i s t h e r e a s i m p l e r w a y t o

c a l c u l a t t h o s e v a l u e s

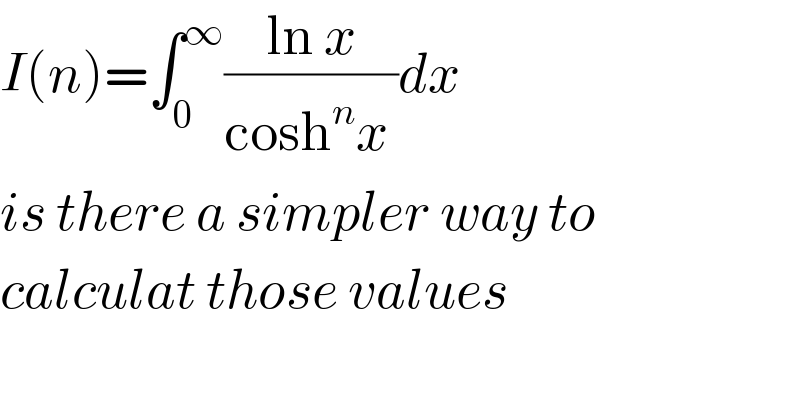
Answered by Aziztisffola last updated on 14/Jul/20

you can use L aplace transform, {it}^{'} s

the best way to do that, mybe there are

the others .

Commented by frc2crc last updated on 14/Jul/20

i {c o u l d n}^{'} t f i n d a n y t h i n g

Commented by mathmax by abdo last updated on 15/Jul/20

can you take a try sir aziz \dots

Commented by Aziztisffola last updated on 16/Jul/20

I try it but I {don}^{'} t found the solution

right now .