Question Number 160395 by qaz last updated on 29/Nov/21
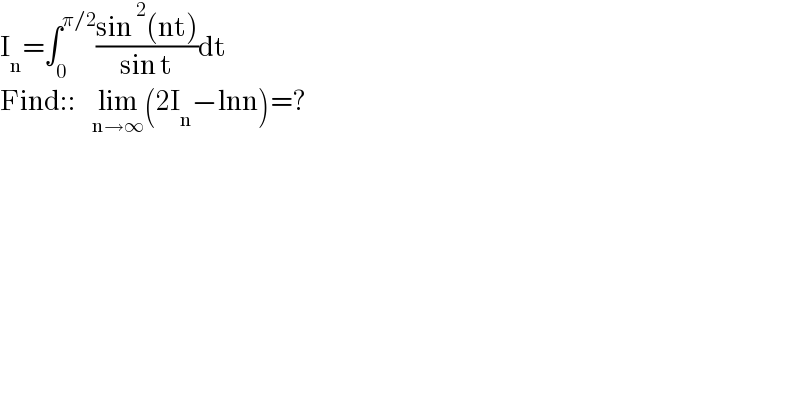
$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{sin}\:^{\mathrm{2}} \left(\mathrm{nt}\right)}{\mathrm{sin}\:\mathrm{t}}\mathrm{dt} \\ $$$$\mathrm{Find}::\:\:\:\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{2I}_{\mathrm{n}} −\mathrm{lnn}\right)=? \\ $$
Answered by Kamel last updated on 29/Nov/21

$$ \\ $$$${I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{2}} \left({nx}\right)}{{sin}\left({x}\right)}{dx} \\ $$$${I}_{{n}+\mathrm{1}} −{I}_{{n}} =\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}{x}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right){sin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\right)}{{sin}\left({x}\right)}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}\left(\left(\mathrm{2}{n}+\mathrm{1}\right){x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\:\:\:\:{I}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}+…+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}+\mathrm{1}={H}_{\mathrm{2}{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}{H}_{{n}} \\ $$$$\:\:\:\:\therefore\:{L}=\:\underset{{n}\rightarrow+\infty} {{lim}}\left(\mathrm{2}{I}_{{n}} −{Ln}\left({n}\right)\right)=\underset{{n}\rightarrow+\infty} {{lim}}\left(\mathrm{2}{H}_{\mathrm{2}{n}+\mathrm{1}} −{H}_{{n}} −{Ln}\left({n}+\mathrm{1}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:=\underset{{n}\rightarrow+\infty} {{lim}}\left(\mathrm{2}\left({H}_{\mathrm{2}{n}+\mathrm{1}} −{Ln}\left(\mathrm{2}{n}+\mathrm{1}\right)\right)+\mathrm{2}{Ln}\left(\mathrm{2}{n}+\mathrm{1}\right)−{H}_{{n}} −{Ln}\left({n}+\mathrm{1}\right)\right) \\ $$$$\:\:\:\:\:\:\:\:=\underset{{n}\rightarrow+\infty} {{lim}}\left(\mathrm{2}\left({H}_{\mathrm{2}{n}+\mathrm{1}} −{Ln}\left(\mathrm{2}{n}+\mathrm{1}\right)\right)+\mathrm{2}{Ln}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{{n}+\mathrm{1}}\right)−\left({H}_{{n}+\mathrm{1}} −{Ln}\left({n}+\mathrm{1}\right)\right)\right) \\ $$$$\:\:\:\:\:\:\:\:=\gamma+\mathrm{2}{Ln}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\therefore\:\:\underset{\boldsymbol{{n}}\rightarrow+\infty} {\boldsymbol{{lim}}}\mathrm{2}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\boldsymbol{{sin}}^{\mathrm{2}} \left(\boldsymbol{{nx}}\right)}{\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right)}\boldsymbol{{dx}}−\boldsymbol{{Ln}}\left(\boldsymbol{{n}}\right)=\mathrm{2}\boldsymbol{{Ln}}\left(\mathrm{2}\right)+\boldsymbol{\gamma} \\ $$$$\:{Where}:\:\boldsymbol{\gamma}=\underset{\boldsymbol{{n}}\rightarrow+\infty} {\boldsymbol{{lim}}}\left(\boldsymbol{{H}}_{\boldsymbol{{n}}} −\boldsymbol{{Ln}}\left(\boldsymbol{{n}}\right)\right)\:{denote}\:{Euler}-{Mascheroni}\:{constant}. \\ $$$$\:\:\:{And}:\:\:{H}_{{n}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+…+\frac{\mathrm{1}}{{n}−\mathrm{1}}+\frac{\mathrm{1}}{{n}}\:\:{the}\:{n}^{{th}} \:{harmonic}\:{number}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{BENAICHA}}\:\boldsymbol{{KAMEL}} \\ $$
Commented by qaz last updated on 30/Nov/21

$$\mathrm{thanks}\:\mathrm{a}\:\mathrm{lot}.\mathrm{very}\:\mathrm{nice}\:\mathrm{solution}. \\ $$
