Question Number 100054 by M±th+et+s last updated on 24/Jun/20
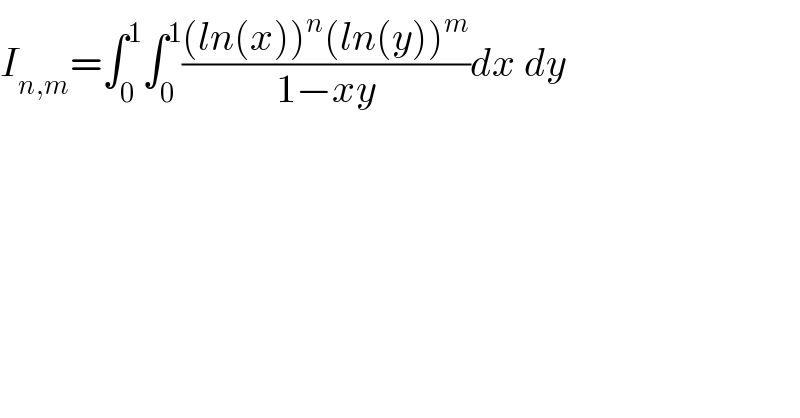
$${I}_{{n},{m}} =\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({ln}\left({x}\right)\right)^{{n}} \left({ln}\left({y}\right)\right)^{{m}} }{\mathrm{1}−{xy}}{dx}\:{dy} \\ $$
Answered by maths mind last updated on 24/Jun/20
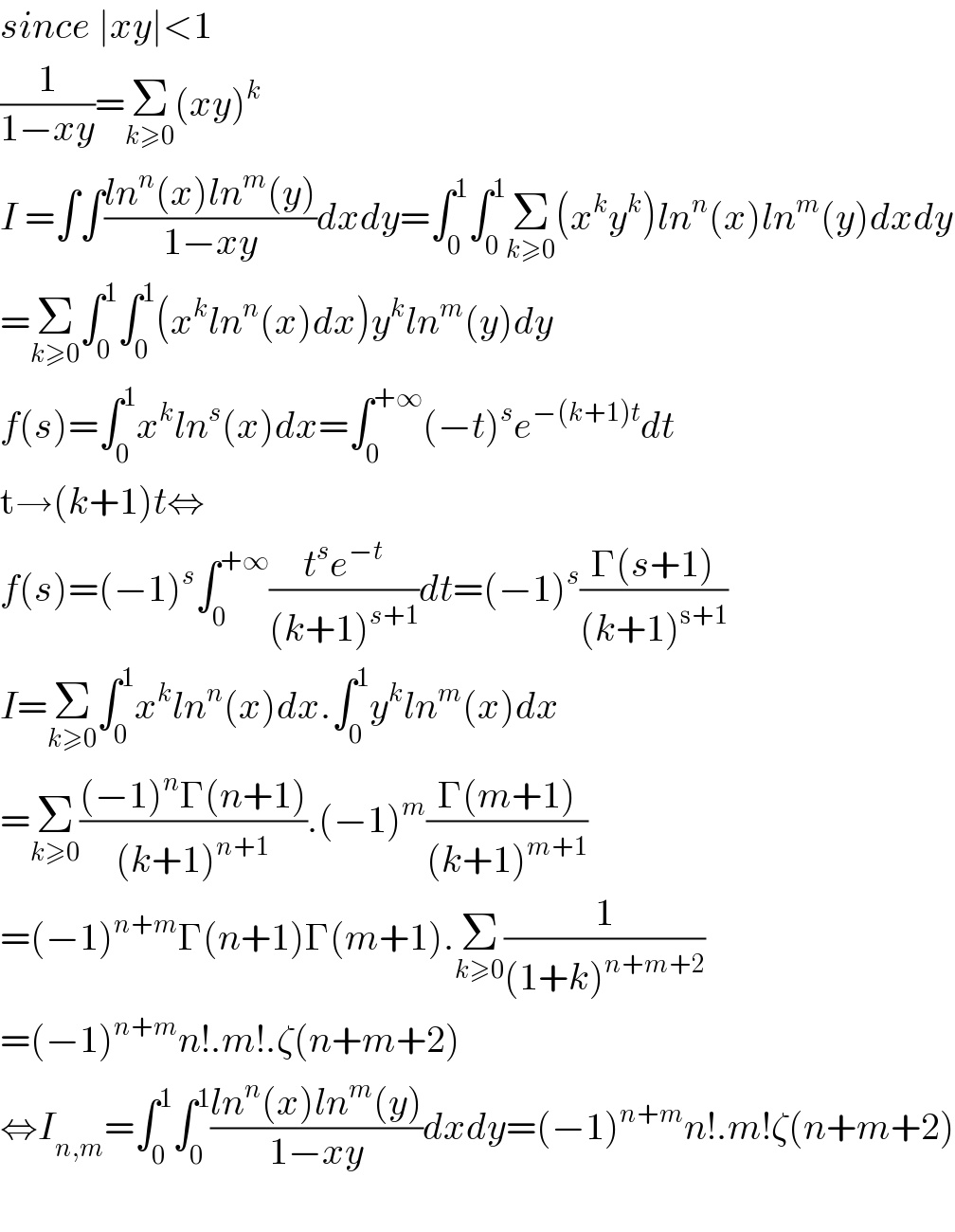
$${since}\:\mid{xy}\mid<\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{xy}}=\underset{{k}\geqslant\mathrm{0}} {\sum}\left({xy}\right)^{{k}} \\ $$$${I}\:=\int\int\frac{{ln}^{{n}} \left({x}\right){ln}^{{m}} \left({y}\right)}{\mathrm{1}−{xy}}{dxdy}=\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \underset{{k}\geqslant\mathrm{0}} {\sum}\left({x}^{{k}} {y}^{{k}} \right){ln}^{{n}} \left({x}\right){ln}^{{m}} \left({y}\right){dxdy} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{{k}} {ln}^{{n}} \left({x}\right){dx}\right){y}^{{k}} {ln}^{{m}} \left({y}\right){dy} \\ $$$${f}\left({s}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {ln}^{{s}} \left({x}\right){dx}=\int_{\mathrm{0}} ^{+\infty} \left(−{t}\right)^{{s}} {e}^{−\left({k}+\mathrm{1}\right){t}} {dt} \\ $$$$\mathrm{t}\rightarrow\left({k}+\mathrm{1}\right){t}\Leftrightarrow \\ $$$${f}\left({s}\right)=\left(−\mathrm{1}\right)^{{s}} \int_{\mathrm{0}} ^{+\infty} \frac{{t}^{{s}} {e}^{−{t}} }{\left({k}+\mathrm{1}\right)^{{s}+\mathrm{1}} }{dt}=\left(−\mathrm{1}\right)^{{s}} \frac{\Gamma\left({s}+\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)^{\mathrm{s}+\mathrm{1}} } \\ $$$${I}=\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {ln}^{{n}} \left({x}\right){dx}.\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{{k}} {ln}^{{m}} \left({x}\right){dx} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} \Gamma\left({n}+\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)^{{n}+\mathrm{1}} }.\left(−\mathrm{1}\right)^{{m}} \frac{\Gamma\left({m}+\mathrm{1}\right)}{\left({k}+\mathrm{1}\right)^{{m}+\mathrm{1}} } \\ $$$$=\left(−\mathrm{1}\right)^{{n}+{m}} \Gamma\left({n}+\mathrm{1}\right)\Gamma\left({m}+\mathrm{1}\right).\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{1}+{k}\right)^{{n}+{m}+\mathrm{2}} } \\ $$$$=\left(−\mathrm{1}\right)^{{n}+{m}} {n}!.{m}!.\zeta\left({n}+{m}+\mathrm{2}\right) \\ $$$$\Leftrightarrow{I}_{{n},{m}} =\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{{n}} \left({x}\right){ln}^{{m}} \left({y}\right)}{\mathrm{1}−{xy}}{dxdy}=\left(−\mathrm{1}\right)^{{n}+{m}} {n}!.{m}!\zeta\left({n}+{m}+\mathrm{2}\right) \\ $$$$ \\ $$
Commented by M±th+et+s last updated on 24/Jun/20
$${cool}\:{sir}.\:{thank}\:{you}\: \\ $$
Commented by maths mind last updated on 24/Jun/20

$${withe}\:{pleasur} \\ $$
