Question Number 144282 by SOMEDAVONG last updated on 24/Jun/21
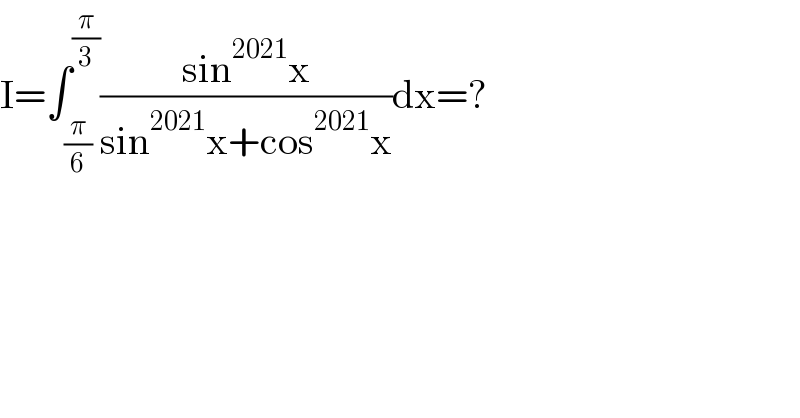
$$\mathrm{I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{sin}^{\mathrm{2021}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2021}} \mathrm{x}+\mathrm{cos}^{\mathrm{2021}} \mathrm{x}}\mathrm{dx}=? \\ $$
Answered by som(math1967) last updated on 24/Jun/21
![I=∫_(π/6) ^(π/3) ((sin^(2021) ((π/3)+(π/6)−x))/(sin^(2021) ((π/3)+(π/6)−x)+cos((π/3)+(π/6)−x)))dx I=∫_(π/6) ^(π/3) ((cos^(2021) x)/(sin^(2021) x+cos^(2021) x))dx ∴2I=∫_(π/6) ^(π/3) ((cos^(2021) x+sin^(2021) x)/(sin^(2021) x+cos^(2021) x))dx 2I=∫_(π/6) ^(π/3) dx I=[(x/2)]_(π/6) ^(π/3) =(π/(12)) ans](https://www.tinkutara.com/question/Q144286.png)
$${I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{{sin}^{\mathrm{2021}} \left(\frac{\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{6}}−{x}\right)}{{sin}^{\mathrm{2021}} \left(\frac{\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{6}}−{x}\right)+{cos}\left(\frac{\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{6}}−{x}\right)}{dx} \\ $$$${I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{{cos}^{\mathrm{2021}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2021}} \mathrm{x}+\mathrm{cos}^{\mathrm{2021}} \mathrm{x}}\mathrm{dx} \\ $$$$\therefore\mathrm{2}{I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{{cos}^{\mathrm{2021}} \mathrm{x}+{sin}^{\mathrm{2021}} {x}}{\mathrm{sin}^{\mathrm{2021}} \mathrm{x}+\mathrm{cos}^{\mathrm{2021}} \mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{2}{I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} {dx} \\ $$$${I}=\left[\frac{{x}}{\mathrm{2}}\right]_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} =\frac{\pi}{\mathrm{12}}\:{ans} \\ $$
Commented by SOMEDAVONG last updated on 24/Jun/21

$$\mathrm{Thanks}\:\mathrm{sir}! \\ $$
