Menu Close

i-Prove-that-sin-3A-3sin-A-4sin-3-A-ii-Show-that-54-satisfies-the-equation-sin-3-cos-2-Hence-or-otherwise-find-the-value-of-sin-54-

Tinku Tara 0 Comments
Pin




Question Number 122007 by ZiYangLee last updated on 13/Nov/20
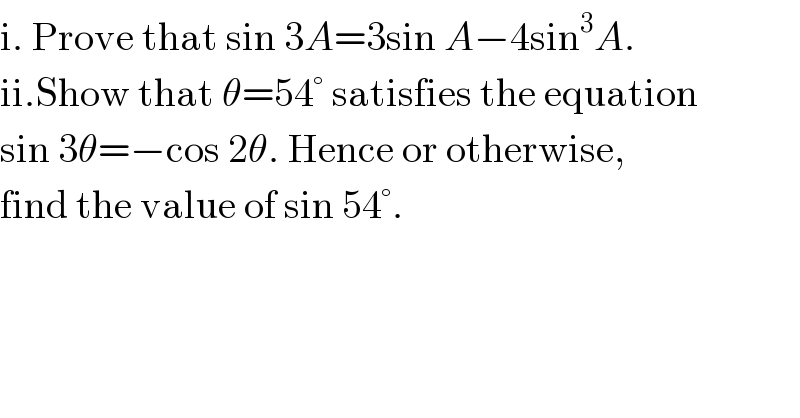
i. Prove that sin 3A=3sin A−4sin^3 A. ii.Show that θ=54° satisfies the equation sin 3θ=−cos 2θ. Hence or otherwise, find the value of sin 54°.
$$\mathrm{i}.\:\mathrm{Prove}\:\mathrm{that}\:\mathrm{sin}\:\mathrm{3}{A}=\mathrm{3sin}\:{A}−\mathrm{4sin}^{\mathrm{3}} {A}. \\ $$$$\mathrm{ii}.\mathrm{Show}\:\mathrm{that}\:\theta=\mathrm{54}°\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{sin}\:\mathrm{3}\theta=−\mathrm{cos}\:\mathrm{2}\theta.\:\mathrm{Hence}\:\mathrm{or}\:\mathrm{otherwise},\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}\:\mathrm{54}°. \\ $$
Answered by TANMAY PANACEA last updated on 13/Nov/20
sin(3A)=sin2AcosA+cos2AsinA =2sinA(1−sin^2 A)+(1−2sin^2 A)sinA =2s−2s^3 +s−2s^3 =3s−4s^3 [s=sinA]
$${sin}\left(\mathrm{3}{A}\right)={sin}\mathrm{2}{AcosA}+{cos}\mathrm{2}{AsinA} \\ $$$$=\mathrm{2}{sinA}\left(\mathrm{1}−{sin}^{\mathrm{2}} {A}\right)+\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {A}\right){sinA} \\ $$$$=\mathrm{2}{s}−\mathrm{2}{s}^{\mathrm{3}} +{s}−\mathrm{2}{s}^{\mathrm{3}} =\mathrm{3}{s}−\mathrm{4}{s}^{\mathrm{3}} \:\:\left[{s}={sinA}\right] \\ $$
Answered by TANMAY PANACEA last updated on 13/Nov/20
LHS sin(3×54)=sin(162)=sin(180−18)=sin18 RHS −cos(108)=−cos(90+18)=−(−sin18)=sin18 so sin3θ=−cos2θ proved sin54=3sin18−4sin^3 18 sin54=3((((√5) −1)/4))−4((((√5) −1)/4))^3
$${LHS}\:{sin}\left(\mathrm{3}×\mathrm{54}\right)={sin}\left(\mathrm{162}\right)={sin}\left(\mathrm{180}−\mathrm{18}\right)={sin}\mathrm{18} \\ $$$${RHS}\:−{cos}\left(\mathrm{108}\right)=−{cos}\left(\mathrm{90}+\mathrm{18}\right)=−\left(−{sin}\mathrm{18}\right)={sin}\mathrm{18} \\ $$$${so}\:{sin}\mathrm{3}\theta=−{cos}\mathrm{2}\theta\:{proved} \\ $$$${sin}\mathrm{54}=\mathrm{3}{sin}\mathrm{18}−\mathrm{4}{sin}^{\mathrm{3}} \mathrm{18} \\ $$$${sin}\mathrm{54}=\mathrm{3}\left(\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{4}}\right)−\mathrm{4}\left(\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} \\ $$
Answered by $@y@m last updated on 13/Nov/20
(i) sin (x+y)=sin xcos y+cos xsin y Put x=2A, y=A sin 3A=sin 2Acos A+cos 2Asin A =(2sinAcos A)cos A+(1−2sin^2 A)sin A =2sinAcos^2 A+sin A−2sin^3 A =2sinA(1−sin^2 A)+sin A−2sin^3 A =2sinA−2sin^3 A+sin A−2sin^3 A =3sinA−4sin^3 A ■■■ (ii) sin (3×54)=sin 162=sin (180−18)=sin 18 −cos (2×54)=−cos 108=−cos (90+18)=sin 18 ■■■ sin 54=sin (3×18) =3sin 18−4sin^3 18 =sin 18(3−4sin^2 18) = (((√5)−1)/4){3−4×((5+1−2(√5))/(16))} = (((√5)−1)/4){3−((6−2(√5))/4)} = (((√5)−1)/4)×((6+2(√5))/4) = ((6(√5)−6+10−2(√5))/(16)) = ((4+4(√5))/(16)) =(((√5)+1)/4)
$$\left({i}\right)\:\mathrm{sin}\:\left({x}+{y}\right)=\mathrm{sin}\:{x}\mathrm{cos}\:{y}+\mathrm{cos}\:{x}\mathrm{sin}\:{y} \\ $$$${Put}\:{x}=\mathrm{2}{A},\:{y}={A} \\ $$$$\mathrm{sin}\:\mathrm{3}{A}=\mathrm{sin}\:\mathrm{2}{A}\mathrm{cos}\:{A}+\mathrm{cos}\:\mathrm{2}{A}\mathrm{sin}\:{A} \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{2sin}{A}\mathrm{cos}\:{A}\right)\mathrm{cos}\:{A}+\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {A}\right)\mathrm{sin}\:{A} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2sin}{A}\mathrm{cos}^{\mathrm{2}} {A}+\mathrm{sin}\:{A}−\mathrm{2sin}^{\mathrm{3}} {A} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2sin}{A}\left(\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {A}\right)+\mathrm{sin}\:{A}−\mathrm{2sin}^{\mathrm{3}} {A} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2sin}{A}−\mathrm{2sin}^{\mathrm{3}} {A}+\mathrm{sin}\:{A}−\mathrm{2sin}^{\mathrm{3}} {A} \\ $$$$\:\:\:\:\:\:\:=\mathrm{3sin}{A}−\mathrm{4sin}^{\mathrm{3}} {A}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\blacksquare\blacksquare\blacksquare \\ $$$$\left({ii}\right)\:\mathrm{sin}\:\left(\mathrm{3}×\mathrm{54}\right)=\mathrm{sin}\:\mathrm{162}=\mathrm{sin}\:\left(\mathrm{180}−\mathrm{18}\right)=\mathrm{sin}\:\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:−\mathrm{cos}\:\left(\mathrm{2}×\mathrm{54}\right)=−\mathrm{cos}\:\mathrm{108}=−\mathrm{cos}\:\left(\mathrm{90}+\mathrm{18}\right)=\mathrm{sin}\:\mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\blacksquare\blacksquare\blacksquare \\ $$$$\mathrm{sin}\:\mathrm{54}=\mathrm{sin}\:\left(\mathrm{3}×\mathrm{18}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3sin}\:\mathrm{18}−\mathrm{4sin}\:^{\mathrm{3}} \mathrm{18} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{sin}\:\mathrm{18}\left(\mathrm{3}−\mathrm{4sin}^{\mathrm{2}} \mathrm{18}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\left\{\mathrm{3}−\mathrm{4}×\frac{\mathrm{5}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\left\{\mathrm{3}−\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{6}\sqrt{\mathrm{5}}−\mathrm{6}+\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{4}+\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$
Commented by ZiYangLee last updated on 16/Nov/20
thanks!
$$\mathrm{thanks}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *