Question Number 122468 by SOMEDAVONG last updated on 17/Nov/20
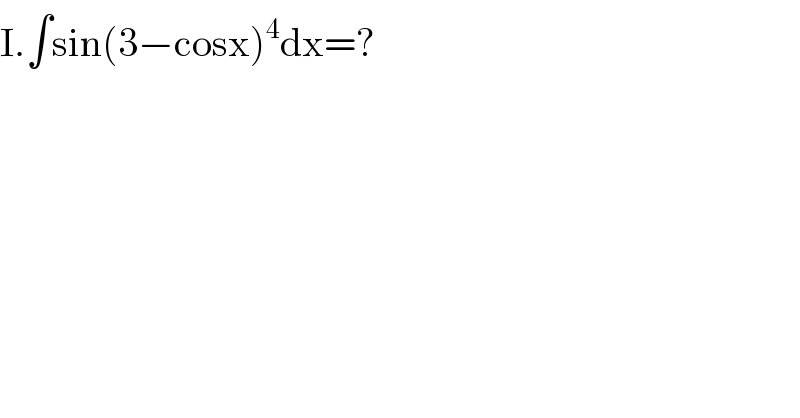
$$\mathrm{I}.\int\mathrm{sin}\left(\mathrm{3}−\mathrm{cosx}\right)^{\mathrm{4}} \mathrm{dx}=? \\ $$
Answered by Dwaipayan Shikari last updated on 17/Nov/20
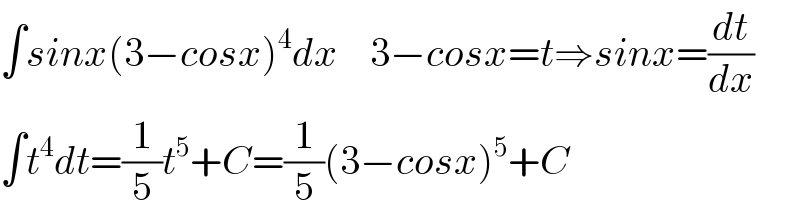
$$\int{sinx}\left(\mathrm{3}−{cosx}\right)^{\mathrm{4}} {dx}\:\:\:\:\mathrm{3}−{cosx}={t}\Rightarrow{sinx}=\frac{{dt}}{{dx}} \\ $$$$\int{t}^{\mathrm{4}} {dt}=\frac{\mathrm{1}}{\mathrm{5}}{t}^{\mathrm{5}} +{C}=\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{3}−{cosx}\right)^{\mathrm{5}} +{C} \\ $$
