Question Number 61522 by YSN 1905 last updated on 03/Jun/19
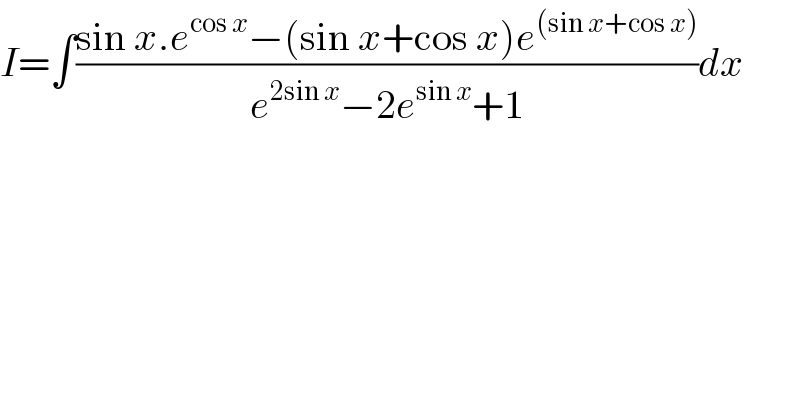
$${I}=\int\frac{\mathrm{sin}\:{x}.{e}^{\mathrm{cos}\:{x}} −\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right){e}^{\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)} }{{e}^{\mathrm{2sin}\:{x}} −\mathrm{2}{e}^{\mathrm{sin}\:{x}} +\mathrm{1}}{dx} \\ $$
Answered by perlman last updated on 04/Jun/19
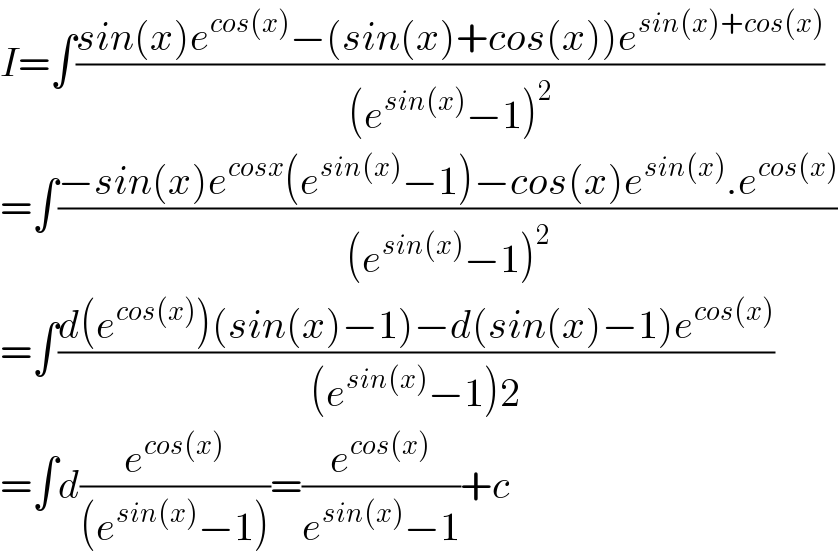
$${I}=\int\frac{{sin}\left({x}\right){e}^{{cos}\left({x}\right)} −\left({sin}\left({x}\right)+{cos}\left({x}\right)\right){e}^{{sin}\left({x}\right)+{cos}\left({x}\right)} }{\left({e}^{{sin}\left({x}\right)} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\int\frac{−{sin}\left({x}\right){e}^{{cosx}} \left({e}^{{sin}\left({x}\right)} −\mathrm{1}\right)−{cos}\left({x}\right){e}^{{sin}\left({x}\right)} .{e}^{{cos}\left({x}\right)} }{\left({e}^{{sin}\left({x}\right)} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\int\frac{{d}\left({e}^{{cos}\left({x}\right)} \right)\left({sin}\left({x}\right)−\mathrm{1}\right)−{d}\left({sin}\left({x}\right)−\mathrm{1}\right){e}^{{cos}\left({x}\right)} }{\left({e}^{{sin}\left({x}\right)} −\mathrm{1}\right)\mathrm{2}} \\ $$$$=\int{d}\frac{{e}^{{cos}\left({x}\right)} }{\left({e}^{{sin}\left({x}\right)} −\mathrm{1}\right)}=\frac{{e}^{{cos}\left({x}\right)} }{{e}^{{sin}\left({x}\right)} −\mathrm{1}}+{c} \\ $$
