i-was-evaluating-lim-x-x-x-1-x-1-log-x-and-got-0-as-the-product-is-it-true-My-Fellows-

Question Number 50954 by afachri last updated on 22/Dec/18

$$\mathrm{i}\:\mathrm{was}\:\mathrm{evaluating}\: \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}\left(\sqrt[{{x}}]{{x}^{} }\:−\:\mathrm{1}\right)}{\mathrm{log}\:{x}} \\ $$$$\mathrm{and}\:\mathrm{got}\:\mathrm{0}\:\mathrm{as}\:\mathrm{the}\:\mathrm{product}.\:\mathrm{is}\:\mathrm{it}\:\mathrm{true},\:\mathrm{My}\:\mathrm{Fellows}\:?? \\ $$

Commented by Abdo msup. last updated on 23/Dec/18

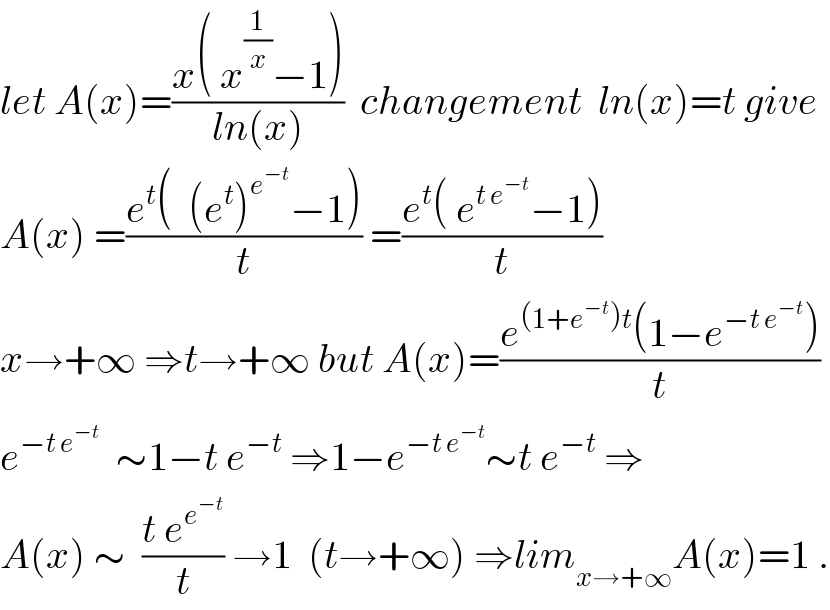
let A(x)=((x( x^(1/x) −1))/(ln(x))) changement ln(x)=t give A(x) =((e^t ( (e^t )^e^(−t) −1))/t) =((e^t ( e^(t e^(−t) ) −1))/t) x→+∞ ⇒t→+∞ but A(x)=((e^((1+e^(−t) )t) (1−e^(−t e^(−t) ) ))/t) e^(−t e^(−t) ) ∼1−t e^(−t) ⇒1−e^(−t e^(−t) ) ∼t e^(−t) ⇒ A(x) ∼ ((t e^e^(−t) )/t) →1 (t→+∞) ⇒lim_(x→+∞) A(x)=1 .

$${let}\:{A}\left({x}\right)=\frac{{x}\left(\:{x}^{\frac{\mathrm{1}}{{x}}} −\mathrm{1}\right)}{{ln}\left({x}\right)}\:\:{changement}\:\:{ln}\left({x}\right)={t}\:{give} \\ $$$${A}\left({x}\right)\:=\frac{{e}^{{t}} \left(\:\:\left({e}^{{t}} \right)^{{e}^{−{t}} } −\mathrm{1}\right)}{{t}}\:=\frac{{e}^{{t}} \left(\:{e}^{{t}\:{e}^{−{t}} } −\mathrm{1}\right)}{{t}} \\ $$$${x}\rightarrow+\infty\:\Rightarrow{t}\rightarrow+\infty\:{but}\:{A}\left({x}\right)=\frac{{e}^{\left(\mathrm{1}+{e}^{−{t}} \right){t}} \left(\mathrm{1}−{e}^{−{t}\:{e}^{−{t}} } \right)}{{t}} \\ $$$${e}^{−{t}\:{e}^{−{t}} } \:\:\sim\mathrm{1}−{t}\:{e}^{−{t}} \:\Rightarrow\mathrm{1}−{e}^{−{t}\:{e}^{−{t}} } \sim{t}\:{e}^{−{t}} \:\Rightarrow \\ $$$${A}\left({x}\right)\:\sim\:\:\frac{{t}\:{e}^{{e}^{−{t}} } }{{t}}\:\rightarrow\mathrm{1}\:\:\left({t}\rightarrow+\infty\right)\:\Rightarrow{lim}_{{x}\rightarrow+\infty} {A}\left({x}\right)=\mathrm{1}\:. \\ $$

Commented by afachri last updated on 24/Dec/18

$$\mathrm{thnk}\:\mathrm{you}\:\mathrm{Sir} \\ $$

Answered by Smail last updated on 22/Dec/18

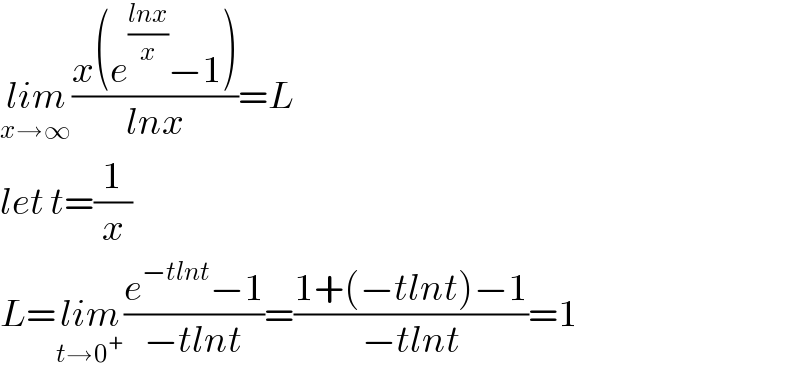
lim_(x→∞) ((x(e^((lnx)/x) −1))/(lnx))=L let t=(1/x) L=lim_(t→0^+ ) ((e^(−tlnt) −1)/(−tlnt))=((1+(−tlnt)−1)/(−tlnt))=1

$$\underset{{x}\rightarrow\infty} {{lim}}\frac{{x}\left({e}^{\frac{{lnx}}{{x}}} −\mathrm{1}\right)}{{lnx}}={L} \\ $$$${let}\:{t}=\frac{\mathrm{1}}{{x}} \\ $$$${L}=\underset{{t}\rightarrow\mathrm{0}^{+} } {{lim}}\frac{{e}^{−{tlnt}} −\mathrm{1}}{−{tlnt}}=\frac{\mathrm{1}+\left(−{tlnt}\right)−\mathrm{1}}{−{tlnt}}=\mathrm{1} \\ $$

Commented by afachri last updated on 22/Dec/18

Thanks alot for answer Mr Smail. i will figure to understand it. thank you very much.

$$\mathrm{Thanks}\:\mathrm{alot}\:\mathrm{for}\:\mathrm{answer}\:\mathrm{Mr}\:\mathrm{Smail}.\:\mathrm{i}\:\mathrm{will}\: \\ $$$$\mathrm{figure}\:\mathrm{to}\:\mathrm{understand}\:\mathrm{it}.\:\mathrm{thank}\:\mathrm{you}\:\mathrm{very} \\ $$$$\mathrm{much}. \\ $$

Commented by afachri last updated on 22/Dec/18

Mr Smail, why (1/(log x)) = (1/(ln x )) ???? I think they have different basic log number. Would you be kind explain to me ????

$$\mathrm{Mr}\:\mathrm{Smail},\:\mathrm{why}\:\frac{\mathrm{1}}{\mathrm{log}\:{x}}\:=\:\frac{\mathrm{1}}{\mathrm{ln}\:{x}\:}\:\:???? \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{they}\:\mathrm{have}\:\mathrm{different}\:\mathrm{basic}\:\mathrm{log}\: \\ $$$$\mathrm{number}.\:\mathrm{Would}\:\mathrm{you}\:\mathrm{be}\:\mathrm{kind}\:\mathrm{explain} \\ $$$$\mathrm{to}\:\mathrm{me}\:???? \\ $$

Commented by Smail last updated on 23/Dec/18

Some people use log instead of ln, so I thought that you did the same here. log(x)=log_(10) (x)=((lnx)/(ln(10))) So the answer would be lim_(t→0^+ ) ((e^(−tlnt) −1)/(−t((ln(t))/(ln(10)))))=lim_(t→0^+ ) ((1−tlnt−1)/(−tlnt))×ln(10) =ln(10)

$${Some}\:{people}\:{use}\:{log}\:{instead}\:{of}\:{ln},\:{so}\:{I}\:{thought}\: \\ $$$${that}\:{you}\:{did}\:{the}\:{same}\:{here}. \\ $$$${log}\left({x}\right)={log}_{\mathrm{10}} \left({x}\right)=\frac{{lnx}}{{ln}\left(\mathrm{10}\right)} \\ $$$${So}\:{the}\:{answer}\:{would}\:{be} \\ $$$$\underset{{t}\rightarrow\mathrm{0}^{+} } {{lim}}\frac{{e}^{−{tlnt}} −\mathrm{1}}{−{t}\frac{{ln}\left({t}\right)}{{ln}\left(\mathrm{10}\right)}}=\underset{{t}\rightarrow\mathrm{0}^{+} } {{lim}}\frac{\mathrm{1}−{tlnt}−\mathrm{1}}{−{tlnt}}×{ln}\left(\mathrm{10}\right) \\ $$$$={ln}\left(\mathrm{10}\right) \\ $$

Commented by afachri last updated on 23/Dec/18

$$\left.\mathrm{Ok}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{Mr}\:\mathrm{Smail}.\::\right) \\ $$

Facebook Tweet Pin

i-was-evaluating-lim-x-x-x-1-x-1-log-x-and-got-0-as-the-product-is-it-true-My-Fellows-

Leave a Reply Cancel reply