Question Number 108018 by Ar Brandon last updated on 13/Aug/20
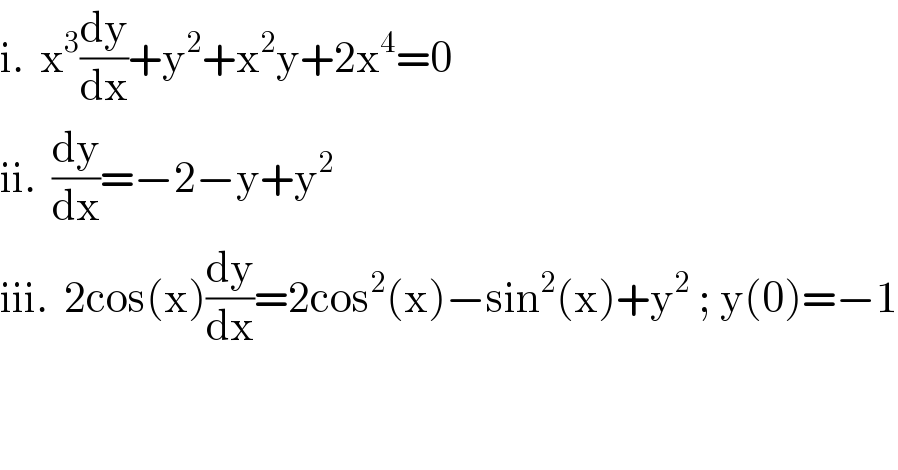
$$\mathrm{i}.\:\:\mathrm{x}^{\mathrm{3}} \frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{y}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{y}+\mathrm{2x}^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{ii}.\:\:\frac{\mathrm{dy}}{\mathrm{dx}}=−\mathrm{2}−\mathrm{y}+\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{iii}.\:\:\mathrm{2cos}\left(\mathrm{x}\right)\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{2cos}^{\mathrm{2}} \left(\mathrm{x}\right)−\mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)+\mathrm{y}^{\mathrm{2}} \:;\:\mathrm{y}\left(\mathrm{0}\right)=−\mathrm{1} \\ $$
Answered by john santu last updated on 14/Aug/20
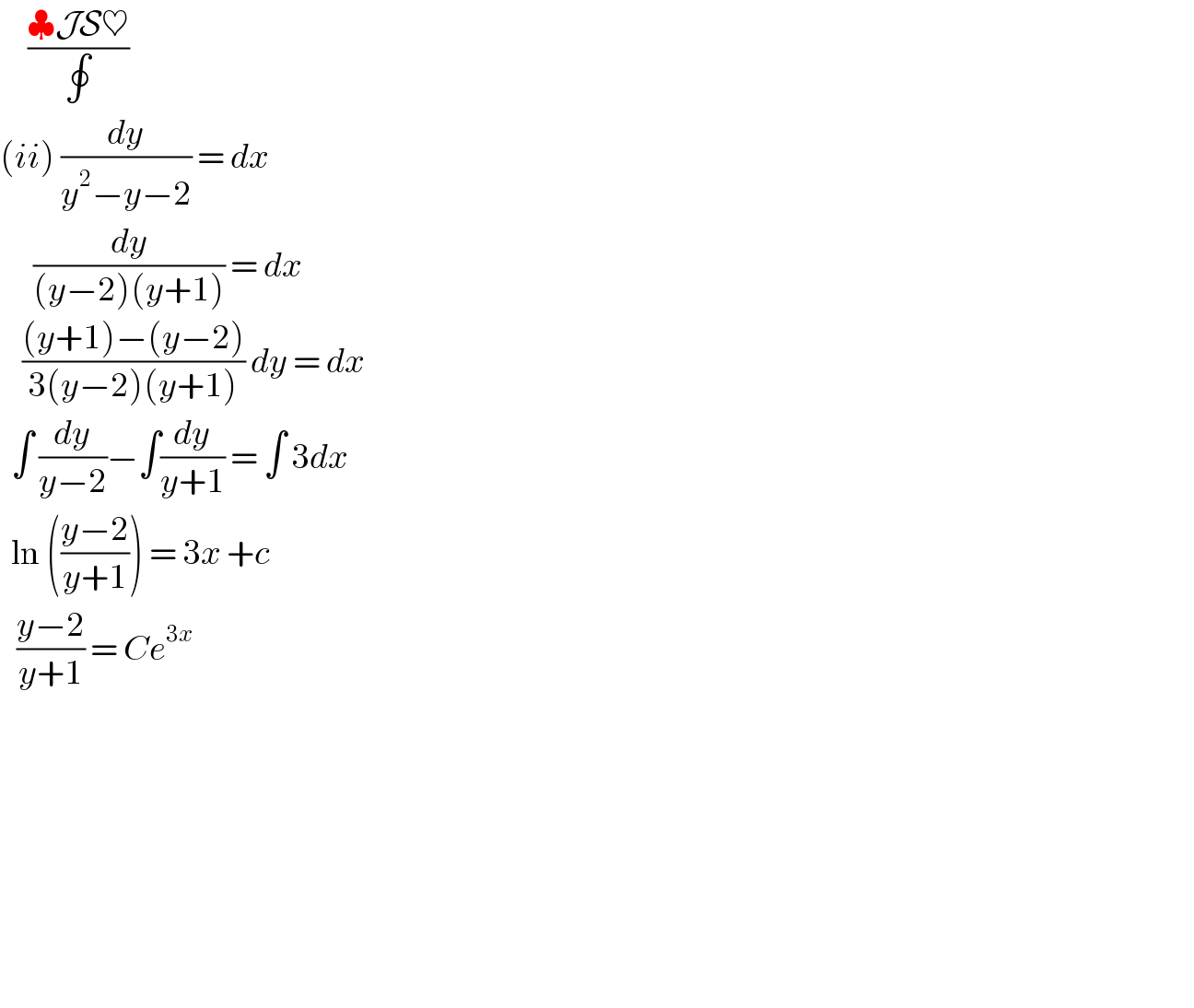
$$\:\:\:\:\:\frac{\clubsuit\mathcal{JS}\heartsuit}{\oint} \\ $$$$\left({ii}\right)\:\frac{{dy}}{{y}^{\mathrm{2}} −{y}−\mathrm{2}}\:=\:{dx} \\ $$$$\:\:\:\:\:\:\frac{{dy}}{\left({y}−\mathrm{2}\right)\left({y}+\mathrm{1}\right)}\:=\:{dx} \\ $$$$\:\:\:\:\frac{\left({y}+\mathrm{1}\right)−\left({y}−\mathrm{2}\right)}{\mathrm{3}\left({y}−\mathrm{2}\right)\left({y}+\mathrm{1}\right)}\:{dy}\:=\:{dx} \\ $$$$\:\:\int\:\frac{{dy}}{{y}−\mathrm{2}}−\int\frac{{dy}}{{y}+\mathrm{1}}\:=\:\int\:\mathrm{3}{dx} \\ $$$$\:\:\mathrm{ln}\:\left(\frac{{y}−\mathrm{2}}{{y}+\mathrm{1}}\right)\:=\:\mathrm{3}{x}\:+{c}\: \\ $$$$\:\:\:\frac{{y}−\mathrm{2}}{{y}+\mathrm{1}}\:=\:{Ce}^{\mathrm{3}{x}} \: \\ $$$$ \\ $$
