Question Number 151287 by yeti123 last updated on 19/Aug/21
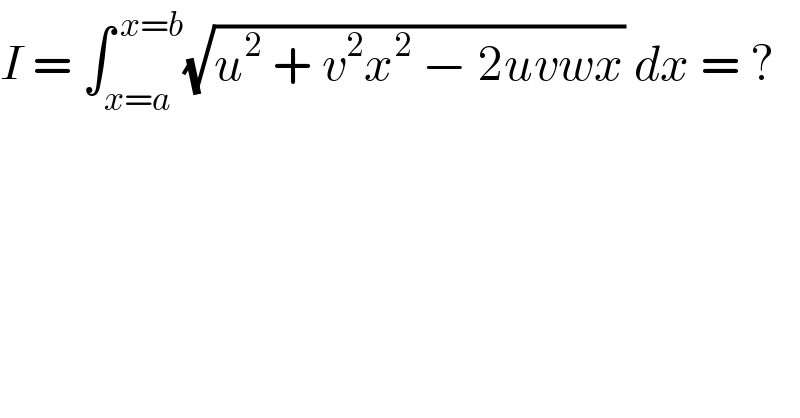
$${I}\:=\:\int_{{x}={a}} ^{\:{x}={b}} \sqrt{{u}^{\mathrm{2}} \:+\:{v}^{\mathrm{2}} {x}^{\mathrm{2}} \:−\:\mathrm{2}{uvwx}}\:{dx}\:=\:? \\ $$
Commented by MJS_new last updated on 19/Aug/21
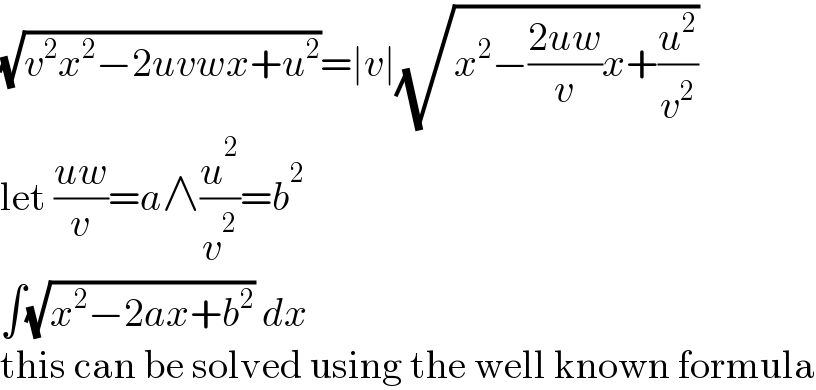
$$\sqrt{{v}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{2}{uvwx}+{u}^{\mathrm{2}} }=\mid{v}\mid\sqrt{{x}^{\mathrm{2}} −\frac{\mathrm{2}{uw}}{{v}}{x}+\frac{{u}^{\mathrm{2}} }{{v}^{\mathrm{2}} }} \\ $$$$\mathrm{let}\:\frac{{uw}}{{v}}={a}\wedge\frac{{u}^{\mathrm{2}} }{{v}^{\mathrm{2}} }={b}^{\mathrm{2}} \\ $$$$\int\sqrt{{x}^{\mathrm{2}} −\mathrm{2}{ax}+{b}^{\mathrm{2}} }\:{dx} \\ $$$$\mathrm{this}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{using}\:\mathrm{the}\:\mathrm{well}\:\mathrm{known}\:\mathrm{formula} \\ $$
Commented by yeti123 last updated on 19/Aug/21

$$\mathrm{I}\:\mathrm{see}!\:\mathrm{thanks}. \\ $$
