Question Number 31839 by Joel578 last updated on 15/Mar/18
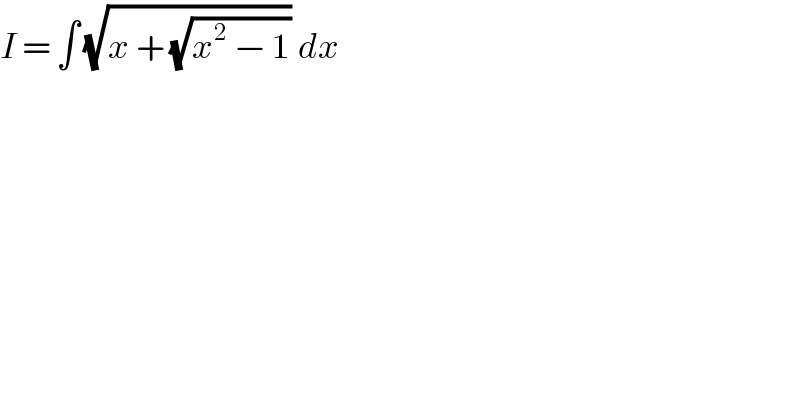
$${I}\:=\:\int\:\sqrt{{x}\:+\:\sqrt{{x}^{\mathrm{2}} \:−\:\mathrm{1}}}\:{dx} \\ $$
Commented by Joel578 last updated on 15/Mar/18
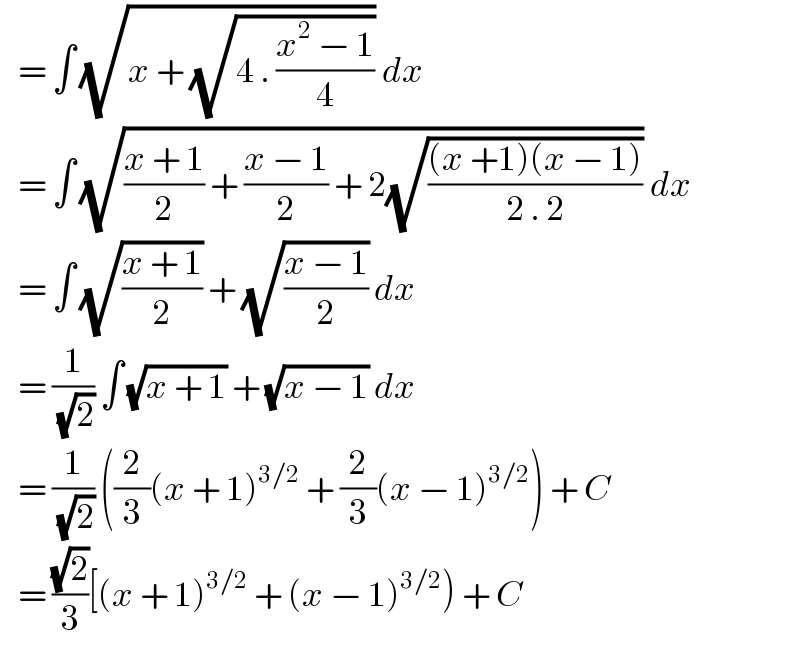
$$\:\:\:=\:\int\:\sqrt{{x}\:+\:\sqrt{\mathrm{4}\:.\:\frac{{x}^{\mathrm{2}} \:−\:\mathrm{1}}{\mathrm{4}}}}\:{dx} \\ $$$$\:\:\:=\:\int\:\sqrt{\frac{{x}\:+\:\mathrm{1}}{\mathrm{2}}\:+\:\frac{{x}\:−\:\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{2}\sqrt{\frac{\left({x}\:+\mathrm{1}\right)\left({x}\:−\:\mathrm{1}\right)}{\mathrm{2}\:.\:\mathrm{2}}}}\:{dx} \\ $$$$\:\:\:=\:\int\:\sqrt{\frac{{x}\:+\:\mathrm{1}}{\mathrm{2}}}\:+\:\sqrt{\frac{{x}\:−\:\mathrm{1}}{\mathrm{2}}}\:{dx} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int\:\sqrt{{x}\:+\:\mathrm{1}}\:+\:\sqrt{{x}\:−\:\mathrm{1}}\:{dx} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\left(\frac{\mathrm{2}}{\mathrm{3}}\left({x}\:+\:\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \:+\:\frac{\mathrm{2}}{\mathrm{3}}\left({x}\:−\:\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \right)\:+\:{C} \\ $$$$\:\:\:=\:\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\left[\left({x}\:+\:\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \:+\:\left({x}\:−\:\mathrm{1}\right)^{\mathrm{3}/\mathrm{2}} \right)\:+\:{C} \\ $$
