Question Number 155237 by mnjuly1970 last updated on 27/Sep/21
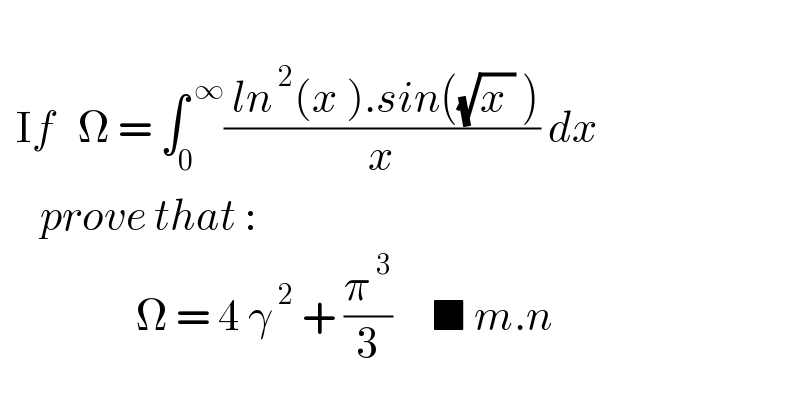
$$ \\ $$$$\:\:\mathrm{I}{f}\:\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{ln}^{\:\mathrm{2}} \left({x}\:\right).{sin}\left(\sqrt{{x}\:}\:\right)}{{x}}\:{dx} \\ $$$$\:\:\:\:\:{prove}\:{that}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega\:=\:\mathrm{4}\:\gamma^{\:\mathrm{2}} \:+\:\frac{\pi^{\:\mathrm{3}} }{\mathrm{3}}\:\:\:\:\:\blacksquare\:{m}.{n} \\ $$
Answered by phanphuoc last updated on 27/Sep/21
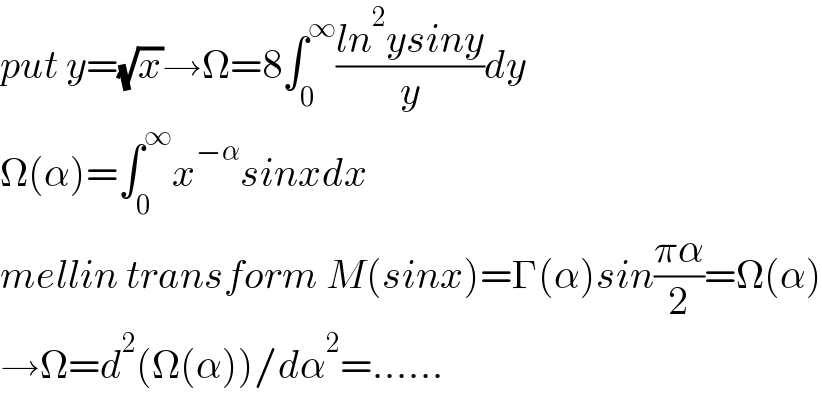
$${put}\:{y}=\sqrt{{x}}\rightarrow\Omega=\mathrm{8}\int_{\mathrm{0}} ^{\infty} \frac{{ln}^{\mathrm{2}} {ysiny}}{{y}}{dy} \\ $$$$\Omega\left(\alpha\right)=\int_{\mathrm{0}} ^{\infty} {x}^{−\alpha} {sinxdx} \\ $$$${mellin}\:{transform}\:{M}\left({sinx}\right)=\Gamma\left(\alpha\right){sin}\frac{\pi\alpha}{\mathrm{2}}=\Omega\left(\alpha\right) \\ $$$$\rightarrow\Omega={d}^{\mathrm{2}} \left(\Omega\left(\alpha\right)\right)/{d}\alpha^{\mathrm{2}} =…… \\ $$
