Question Number 157585 by MathSh last updated on 24/Oct/21
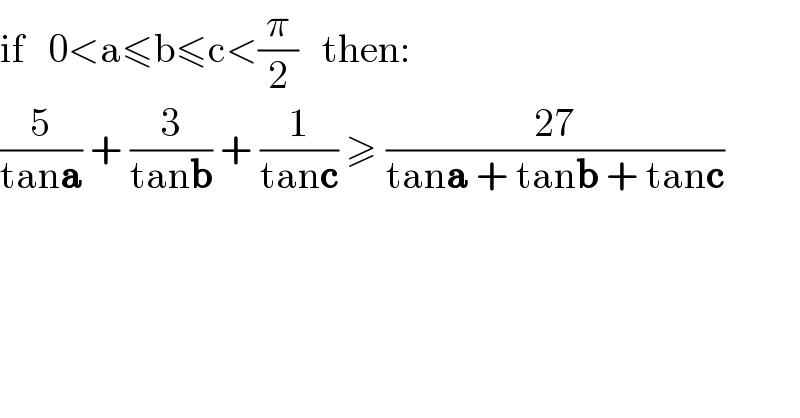
$$\mathrm{if}\:\:\:\mathrm{0}<\mathrm{a}\leqslant\mathrm{b}\leqslant\mathrm{c}<\frac{\pi}{\mathrm{2}}\:\:\:\mathrm{then}: \\ $$$$\frac{\mathrm{5}}{\mathrm{tan}\boldsymbol{\mathrm{a}}}\:+\:\frac{\mathrm{3}}{\mathrm{tan}\boldsymbol{\mathrm{b}}}\:+\:\frac{\mathrm{1}}{\mathrm{tan}\boldsymbol{\mathrm{c}}}\:\geqslant\:\frac{\mathrm{27}}{\mathrm{tan}\boldsymbol{\mathrm{a}}\:+\:\mathrm{tan}\boldsymbol{\mathrm{b}}\:+\:\mathrm{tan}\boldsymbol{\mathrm{c}}} \\ $$
Answered by ghimisi last updated on 25/Oct/21
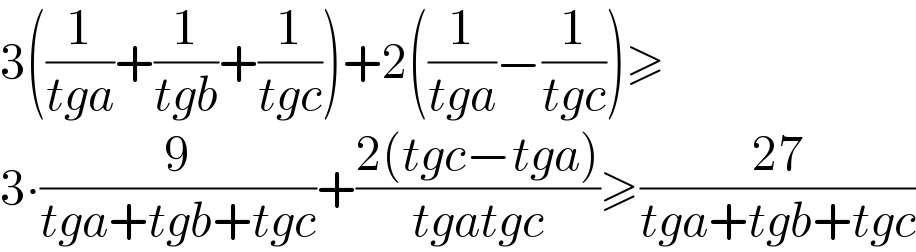
$$\mathrm{3}\left(\frac{\mathrm{1}}{{tga}}+\frac{\mathrm{1}}{{tgb}}+\frac{\mathrm{1}}{{tgc}}\right)+\mathrm{2}\left(\frac{\mathrm{1}}{{tga}}−\frac{\mathrm{1}}{{tgc}}\right)\geqslant \\ $$$$\mathrm{3}\centerdot\frac{\mathrm{9}}{{tga}+{tgb}+{tgc}}+\frac{\mathrm{2}\left({tgc}−{tga}\right)}{{tgatgc}}\geqslant\frac{\mathrm{27}}{{tga}+{tgb}+{tgc}} \\ $$
Commented by MathSh last updated on 25/Oct/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er}\:\mathrm{very}\:\mathrm{nice} \\ $$
