Question Number 116359 by bemath last updated on 03/Oct/20
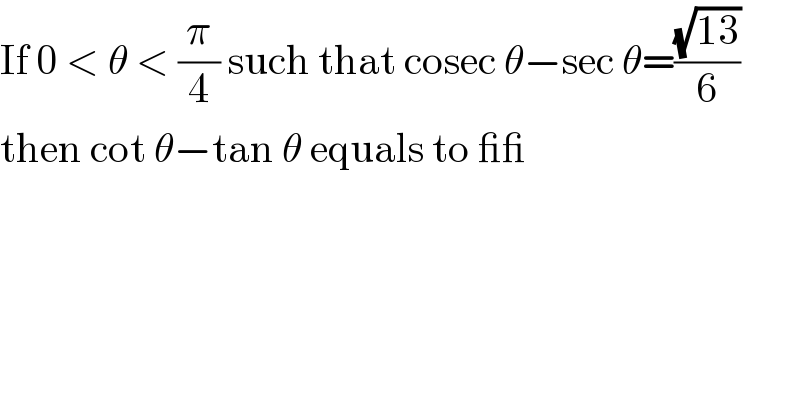
$$\mathrm{If}\:\mathrm{0}\:<\:\theta\:<\:\frac{\pi}{\mathrm{4}}\:\mathrm{such}\:\mathrm{that}\:\mathrm{cosec}\:\theta−\mathrm{sec}\:\theta=\frac{\sqrt{\mathrm{13}}}{\mathrm{6}} \\ $$$$\mathrm{then}\:\mathrm{cot}\:\theta−\mathrm{tan}\:\theta\:\mathrm{equals}\:\mathrm{to}\:\_\_ \\ $$
Answered by bobhans last updated on 03/Oct/20

$$\Rightarrow\:\mathrm{let}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:=\:\mathrm{r}\:.\:\mathrm{Then}\:\left(\frac{\mathrm{1}}{\mathrm{sin}\:\theta}\:−\frac{\mathrm{1}}{\mathrm{cos}\:\theta}\right)^{\mathrm{2}} =\:\frac{\mathrm{13}}{\mathrm{36}} \\ $$$$\Rightarrow\:\frac{\left(\mathrm{cos}\:\theta−\mathrm{sin}\:\theta\right)^{\mathrm{2}} }{\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{13}}{\mathrm{36}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}−\mathrm{2r}}{\mathrm{r}^{\mathrm{2}} }\:=\:\frac{\mathrm{13}}{\mathrm{36}}\:;\:\mathrm{13r}^{\mathrm{2}} +\mathrm{72r}−\mathrm{36}\:=\:\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{13r}−\mathrm{6}\right)\left(\mathrm{r}+\mathrm{6}\right)=\:\mathrm{0}\:\rightarrow\begin{cases}{\mathrm{r}=−\mathrm{6}\left(\mathrm{rejected}\right)}\\{\mathrm{r}=\frac{\mathrm{6}}{\mathrm{13}}}\end{cases} \\ $$$$\mathrm{So}\:\mathrm{we}\:\mathrm{have}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:=\:\frac{\mathrm{6}}{\mathrm{13}}\:\mathrm{and}\:\mathrm{sin}\:\mathrm{2}\theta\:=\:\frac{\mathrm{12}}{\mathrm{13}} \\ $$$$\mathrm{so}\:\mathrm{cot}\:\theta−\mathrm{tan}\:\theta\:=\:\frac{\mathrm{2cos}\:\mathrm{2}\theta}{\mathrm{sin}\:\mathrm{2}\theta}\:=\:\frac{\mathrm{2}×\left(\frac{\mathrm{5}}{\mathrm{13}}\right)}{\left(\frac{\mathrm{12}}{\mathrm{13}}\right)}\:=\:\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$ \\ $$$$ \\ $$
