Question Number 182946 by myint last updated on 17/Dec/22
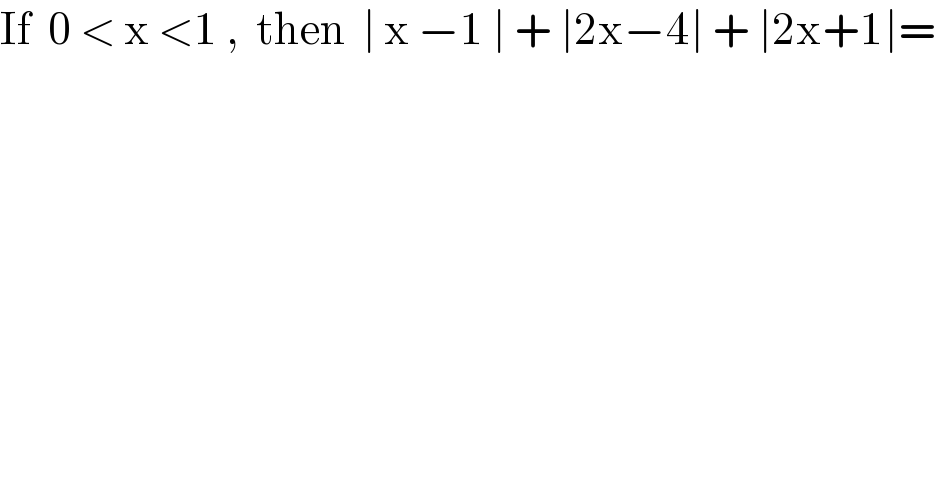
$$\mathrm{If}\:\:\mathrm{0}\:<\:\mathrm{x}\:<\mathrm{1}\:,\:\:\mathrm{then}\:\:\mid\:\mathrm{x}\:−\mathrm{1}\:\mid\:+\:\mid\mathrm{2x}−\mathrm{4}\mid\:+\:\mid\mathrm{2x}+\mathrm{1}\mid= \\ $$
Commented by mr W last updated on 17/Dec/22
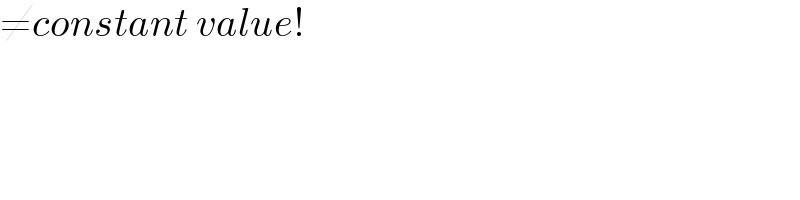
$$\neq{constant}\:{value}! \\ $$
Answered by Frix last updated on 17/Dec/22
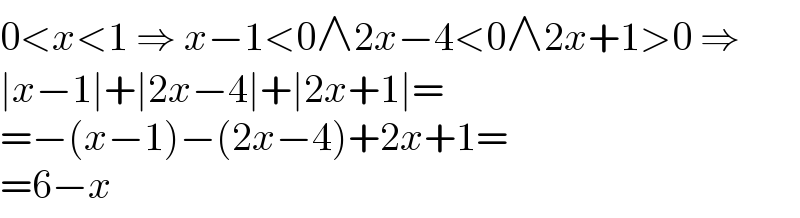
$$\mathrm{0}<{x}<\mathrm{1}\:\Rightarrow\:{x}−\mathrm{1}<\mathrm{0}\wedge\mathrm{2}{x}−\mathrm{4}<\mathrm{0}\wedge\mathrm{2}{x}+\mathrm{1}>\mathrm{0}\:\Rightarrow \\ $$$$\mid{x}−\mathrm{1}\mid+\mid\mathrm{2}{x}−\mathrm{4}\mid+\mid\mathrm{2}{x}+\mathrm{1}\mid= \\ $$$$=−\left({x}−\mathrm{1}\right)−\left(\mathrm{2}{x}−\mathrm{4}\right)+\mathrm{2}{x}+\mathrm{1}= \\ $$$$=\mathrm{6}−{x} \\ $$
