Question Number 32987 by NECx last updated on 08/Apr/18

$${If}\:\mathrm{1}=\mathrm{1} \\ $$$$\mathrm{2}=\mathrm{4} \\ $$$$\mathrm{3}=\mathrm{10}\: \\ $$$$\mathrm{4}=\mathrm{20} \\ $$$$\mathrm{5}=? \\ $$
Answered by MJS last updated on 09/Apr/18

$$\mathrm{one}\:\mathrm{possibility}: \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\mathrm{6}}\left({n}+\mathrm{2}\right)\left({n}+\mathrm{1}\right){n} \\ $$$${a}_{\mathrm{5}} =\mathrm{35} \\ $$$$ \\ $$$$\mathrm{with}\:{k}\:\mathrm{given}\:\mathrm{points}\:\mathrm{a}\:\mathrm{polynome} \\ $$$$\mathrm{function}\:\mathrm{of}\:\mathrm{degree}\:{k}−\mathrm{1}\:\mathrm{is}\:\mathrm{determined} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}: \\ $$$${y}={ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d} \\ $$$$ \\ $$$$\mathrm{1}={a}+{b}+{c}+{d} \\ $$$$\mathrm{4}=\mathrm{8}{a}+\mathrm{4}{b}+\mathrm{2}{c}+{d} \\ $$$$\mathrm{10}=\mathrm{27}{a}+\mathrm{9}{b}+\mathrm{3}{c}+{d} \\ $$$$\mathrm{20}=\mathrm{64}{a}+\mathrm{16}{b}+\mathrm{4}{c}+{d} \\ $$$$ \\ $$$$\mathrm{solving}\:\mathrm{leads}\:\mathrm{to}\: \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{6}};\:{b}=\frac{\mathrm{1}}{\mathrm{2}};\:{c}=\frac{\mathrm{1}}{\mathrm{3}};\:{d}=\mathrm{0} \\ $$
Commented by MJS last updated on 09/Apr/18
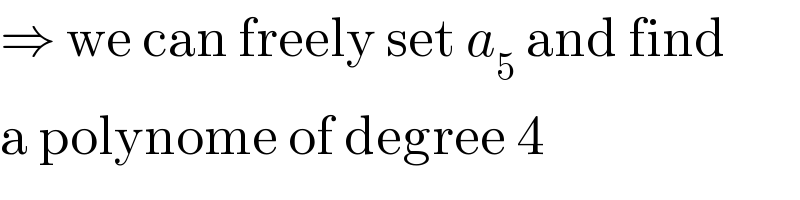
$$\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{freely}\:\mathrm{set}\:{a}_{\mathrm{5}} \:\mathrm{and}\:\mathrm{find} \\ $$$$\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{4} \\ $$
Commented by MJS last updated on 09/Apr/18
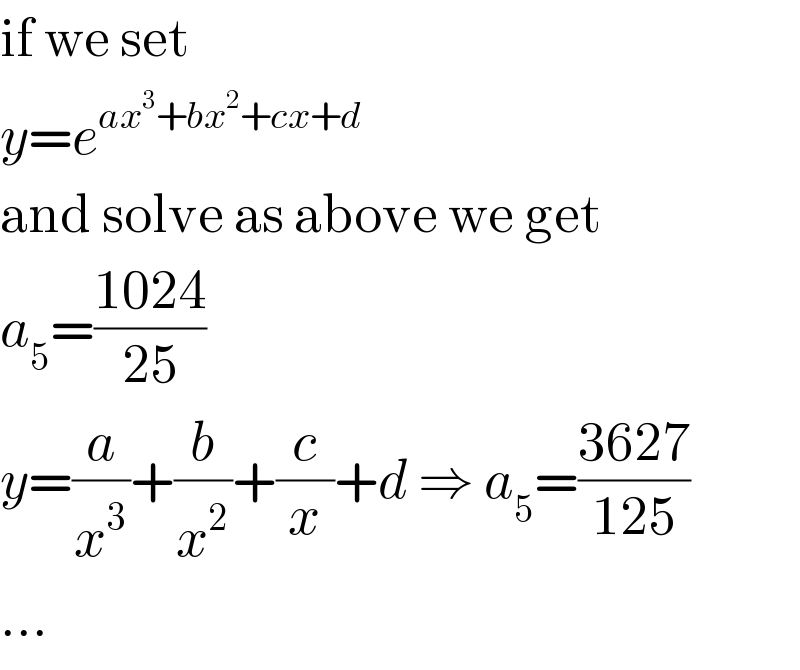
$$\mathrm{if}\:\mathrm{we}\:\mathrm{set} \\ $$$${y}={e}^{{ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}} \\ $$$$\mathrm{and}\:\mathrm{solve}\:\mathrm{as}\:\mathrm{above}\:\mathrm{we}\:\mathrm{get} \\ $$$${a}_{\mathrm{5}} =\frac{\mathrm{1024}}{\mathrm{25}} \\ $$$${y}=\frac{{a}}{{x}^{\mathrm{3}} }+\frac{{b}}{{x}^{\mathrm{2}} }+\frac{{c}}{{x}}+{d}\:\Rightarrow\:{a}_{\mathrm{5}} =\frac{\mathrm{3627}}{\mathrm{125}} \\ $$$$… \\ $$
