Menu Close

if-1-1-x-n-m-0-a-m-x-m-determinate-a-m-

Tinku Tara 0 Comments
Pin




Question Number 98940 by mathmax by abdo last updated on 17/Jun/20
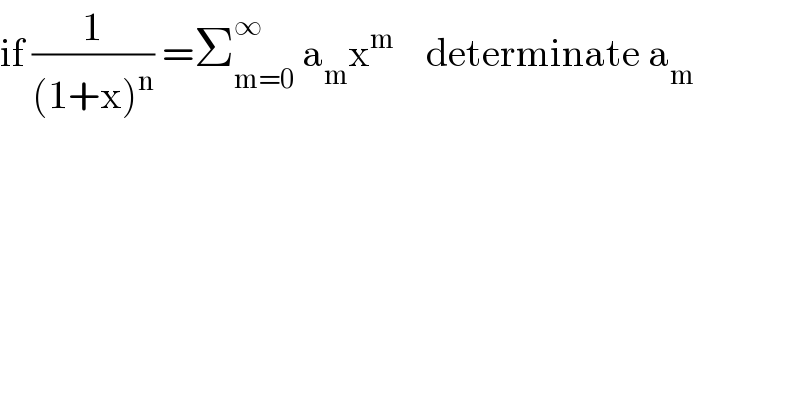
if (1/((1+x)^n )) =Σ_(m=0) ^∞ a_m x^m determinate a_m
$$\mathrm{if}\:\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} }\:=\sum_{\mathrm{m}=\mathrm{0}} ^{\infty} \:\mathrm{a}_{\mathrm{m}} \mathrm{x}^{\mathrm{m}} \:\:\:\:\mathrm{determinate}\:\mathrm{a}_{\mathrm{m}} \\ $$
Commented by mr W last updated on 17/Jun/20
for n≥2: (1/((1+x)^n ))=Σ_(m=0) ^∞ (−1)^m C_(n−1) ^(m+n−1) x^m
$${for}\:{n}\geqslant\mathrm{2}: \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{{n}} }=\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{m}} {C}_{{n}−\mathrm{1}} ^{{m}+{n}−\mathrm{1}} {x}^{{m}} \\ $$
Answered by maths mind last updated on 17/Jun/20
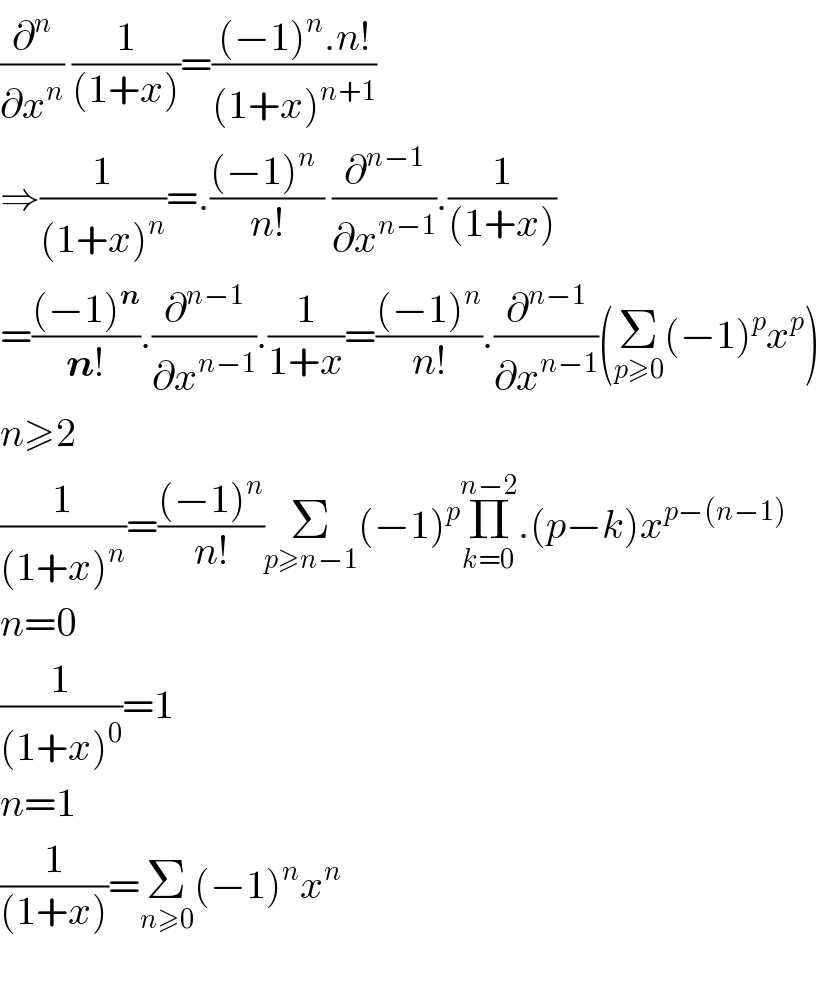
(∂^n /∂x^n ) (1/((1+x)))=(((−1)^n .n!)/((1+x)^(n+1) )) ⇒(1/((1+x)^n ))=.(((−1)^n )/(n!)) (∂^(n−1) /∂x^(n−1) ).(1/((1+x))) =(((−1)^n )/(n!)).(∂^(n−1) /∂x^(n−1) ).(1/(1+x))=(((−1)^n )/(n!)).(∂^(n−1) /∂x^(n−1) )(Σ_(p≥0) (−1)^p x^p ) n≥2 (1/((1+x)^n ))=(((−1)^n )/(n!))Σ_(p≥n−1) (−1)^p Π_(k=0) ^(n−2) .(p−k)x^(p−(n−1)) n=0 (1/((1+x)^0 ))=1 n=1 (1/((1+x)))=Σ_(n≥0) (−1)^n x^n
$$\frac{\partial^{{n}} }{\partial{x}^{{n}} }\:\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)}=\frac{\left(−\mathrm{1}\right)^{{n}} .{n}!}{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{{n}} }=.\frac{\left(−\mathrm{1}\right)^{{n}} \:}{{n}!}\:\frac{\partial^{{n}−\mathrm{1}} }{\partial{x}^{{n}−\mathrm{1}} }.\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} }{\boldsymbol{{n}}!}.\frac{\partial^{{n}−\mathrm{1}} }{\partial{x}^{{n}−\mathrm{1}} }.\frac{\mathrm{1}}{\mathrm{1}+{x}}=\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}.\frac{\partial^{{n}−\mathrm{1}} }{\partial{x}^{{n}−\mathrm{1}} }\left(\underset{{p}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{p}} {x}^{{p}} \right) \\ $$$${n}\geqslant\mathrm{2} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{{n}} }=\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}!}\underset{{p}\geqslant{n}−\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{p}} \underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{2}} {\prod}}.\left({p}−{k}\right){x}^{{p}−\left({n}−\mathrm{1}\right)} \\ $$$${n}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{0}} }=\mathrm{1} \\ $$$${n}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)}=\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 18/Jun/20
thank you sir .
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:. \\ $$
Answered by mathmax by abdo last updated on 18/Jun/20
f(x) =(1/((1+x)^n )) ⇒f(x) =Σ_(m=0) ^∞ ((f^((m)) (0))/(m!)) x^m let determine f^((m)) (0) f(x) =(x+1)^(−n) =(x+1)^p with p =−n ⇒f^((m)) (x) ={(x+1)^p }^((m)) if m>p f^((m)) (x)=0 if m≤p we have f^((1)) (x) =p(x+1)^(p−1) f^((2)) (x) =p(p−1)(x+1)^(p−2) ⇒f^((m)) (x) =p(p−1)...(p−m+1)(x+1)^(p−m) =(−n)(−n−1)....(−n−m+1)(x+1)^(−n−m) = (−1)^m n(n+1)....(n+m−1)(x+1)^(−n−m) ⇒ f(x) =Σ_(m=0) ^n ((f^((m)) (0))/(m!)) x^m =Σ_(m=0) ^n (((−1)^m n(n+1)...(n+m−1))/(m!)) x^m ⇒ a_m =(((−1)^m n(n+1)....(n+m−1))/(m!))
$$\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{n}} }\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{m}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{m}\right)} \left(\mathrm{0}\right)}{\mathrm{m}!}\:\mathrm{x}^{\mathrm{m}} \:\mathrm{let}\:\mathrm{determine}\:\mathrm{f}^{\left(\mathrm{m}\right)} \left(\mathrm{0}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{n}} \:\:=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{p}} \:\:\:\mathrm{with}\:\mathrm{p}\:=−\mathrm{n}\:\Rightarrow\mathrm{f}^{\left(\mathrm{m}\right)} \left(\mathrm{x}\right)\:=\left\{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{p}} \right\}^{\left(\mathrm{m}\right)} \\ $$$$\mathrm{if}\:\mathrm{m}>\mathrm{p}\:\mathrm{f}^{\left(\mathrm{m}\right)} \left(\mathrm{x}\right)=\mathrm{0}\:\:\mathrm{if}\:\mathrm{m}\leqslant\mathrm{p}\:\:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{\left(\mathrm{1}\right)} \left(\mathrm{x}\right)\:=\mathrm{p}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)\:=\mathrm{p}\left(\mathrm{p}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{p}−\mathrm{2}} \:\Rightarrow\mathrm{f}^{\left(\mathrm{m}\right)} \left(\mathrm{x}\right)\:=\mathrm{p}\left(\mathrm{p}−\mathrm{1}\right)…\left(\mathrm{p}−\mathrm{m}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{p}−\mathrm{m}} \\ $$$$=\left(−\mathrm{n}\right)\left(−\mathrm{n}−\mathrm{1}\right)….\left(−\mathrm{n}−\mathrm{m}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{n}−\mathrm{m}} \\ $$$$=\:\left(−\mathrm{1}\right)^{\mathrm{m}} \:\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)….\left(\mathrm{n}+\mathrm{m}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)^{−\mathrm{n}−\mathrm{m}} \:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{m}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\mathrm{f}^{\left(\mathrm{m}\right)} \left(\mathrm{0}\right)}{\mathrm{m}!}\:\mathrm{x}^{\mathrm{m}} \:=\sum_{\mathrm{m}=\mathrm{0}} ^{\mathrm{n}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{m}} \mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)…\left(\mathrm{n}+\mathrm{m}−\mathrm{1}\right)}{\mathrm{m}!}\:\mathrm{x}^{\mathrm{m}} \:\Rightarrow \\ $$$$\mathrm{a}_{\mathrm{m}} =\frac{\left(−\mathrm{1}\right)^{\mathrm{m}} \:\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)….\left(\mathrm{n}+\mathrm{m}−\mathrm{1}\right)}{\mathrm{m}!} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *