Question Number 116595 by ZiYangLee last updated on 05/Oct/20
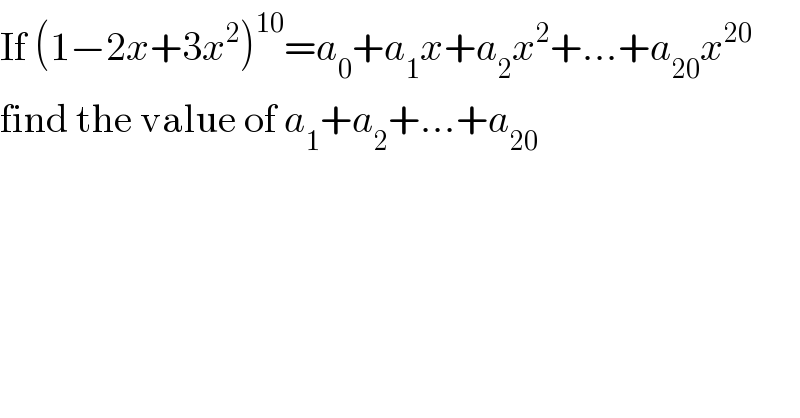
$$\mathrm{If}\:\left(\mathrm{1}−\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} \right)^{\mathrm{10}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} {x}+{a}_{\mathrm{2}} {x}^{\mathrm{2}} +…+{a}_{\mathrm{20}} {x}^{\mathrm{20}} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{\mathrm{20}} \\ $$
Answered by mr W last updated on 05/Oct/20
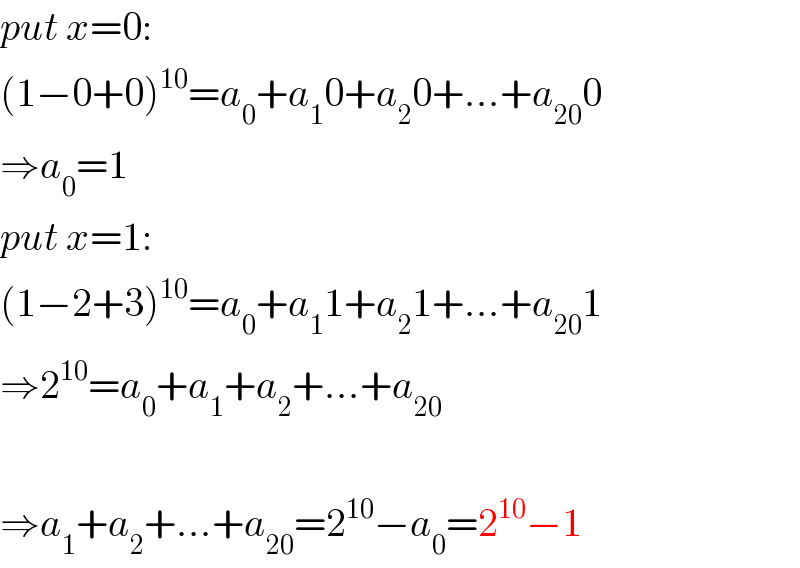
$${put}\:{x}=\mathrm{0}: \\ $$$$\left(\mathrm{1}−\mathrm{0}+\mathrm{0}\right)^{\mathrm{10}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} \mathrm{0}+{a}_{\mathrm{2}} \mathrm{0}+…+{a}_{\mathrm{20}} \mathrm{0} \\ $$$$\Rightarrow{a}_{\mathrm{0}} =\mathrm{1} \\ $$$${put}\:{x}=\mathrm{1}: \\ $$$$\left(\mathrm{1}−\mathrm{2}+\mathrm{3}\right)^{\mathrm{10}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} \mathrm{1}+{a}_{\mathrm{2}} \mathrm{1}+…+{a}_{\mathrm{20}} \mathrm{1} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{10}} ={a}_{\mathrm{0}} +{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{\mathrm{20}} \\ $$$$ \\ $$$$\Rightarrow{a}_{\mathrm{1}} +{a}_{\mathrm{2}} +…+{a}_{\mathrm{20}} =\mathrm{2}^{\mathrm{10}} −{a}_{\mathrm{0}} =\mathrm{2}^{\mathrm{10}} −\mathrm{1} \\ $$
Commented by ZiYangLee last updated on 05/Oct/20

$$\bigstar \\ $$
