If-1-a-1-2a-1-3a-1-b-2-2b-a-and-b-are-positive-integers-Find-minimum-value-of-a-b-

Question Number 21236 by Joel577 last updated on 17/Sep/17

If \frac{1}{a} + \frac{1}{2 a} + \frac{1}{3 a} = \frac{1}{b^{2} - 2 b}

a and b are positive integers

Find minimum value of a + b

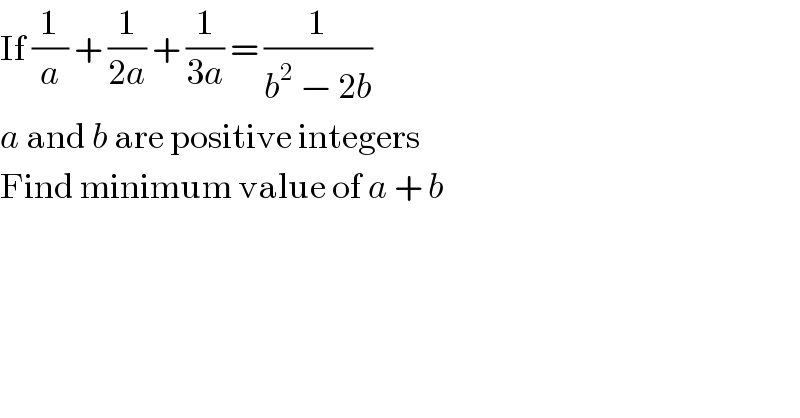
Answered by mrW1 last updated on 17/Sep/17

\frac{1}{a} (1 + \frac{1}{2} + \frac{1}{3}) = \frac{1}{b (b - 2)}

\frac{11}{6 a} = \frac{1}{b (b - 2)}

a = \frac{11 b (b - 2)}{6} = 11 k

b (b - 2) = 6 k

b^{2} - 2 b - 6 k = 0

b = \frac{2 + \sqrt{4 + 4 \times 6 k}}{2} = 1 + \sqrt{1 + 6 k}

\Rightarrow k = 2 i (3 i \pm 1) with i = 1, 2, 3 \dots \dots

\Rightarrow b = 6 i + 1 \pm 1

\Rightarrow a = 22 i (3 i \pm 1)

k = 4, 8, 20, 28, 48, 60 \dots

b = 6, 8, 12, 14, 18, 20 \dots

a = 44, 88, 132, 154, 198, 220 \dots

k_{\min} = 4

b_{\min} = 1 + 5 = 6

a_{\min} = 11 \times 4 = 44

\Rightarrow {(a + b)}_{\min} = 50

Commented by $@ty@m last updated on 17/Sep/17

W i l l y o u p l . e x p l a i n b l u e p a r t ?

Commented by mrW1 last updated on 17/Sep/17

b = 1 + \sqrt{1 + 6 k}

1 + 6 k = j^{2}

k = \frac{j^{2} - 1}{6} = \frac{(j - 1) (j + 1)}{2 \times 3}

j must be odd, i . e . j = 2 m + 1

\Rightarrow k = \frac{2 m (2 m + 2)}{2 \times 3} = \frac{2 m (m + 1)}{3}

m must be 3 i or 3 i - 1

\Rightarrow k = 2 i (3 i + 1) or 2 i (3 i - 1)

\Rightarrow k = 2 i (3 i \pm 1)

b = 1 + \sqrt{1 + 6 k} = 1 + \sqrt{1 + 6 \times 2 i (3 i \pm 1)}

= 1 + \sqrt{{(6 i \pm 1)}^{2}}

= 1 + 6 i \pm 1

a = 11 k = 22 i (3 i \pm 1)

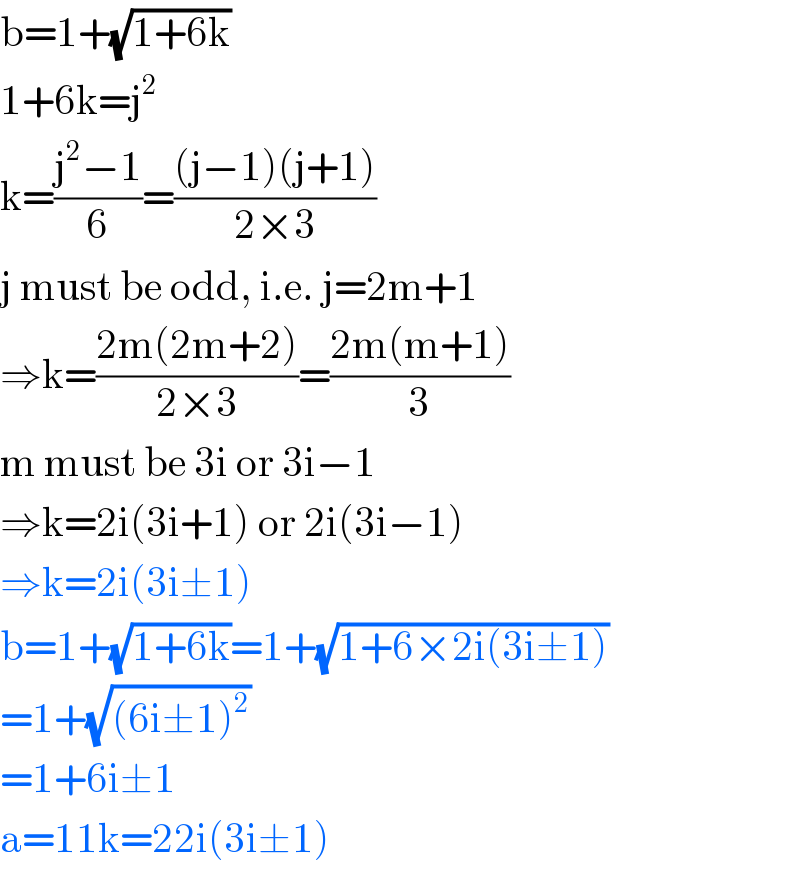
Commented by Joel577 last updated on 18/Sep/17

u n d e r s t o o d . t h a n k y o u v e r y m u c h

Facebook Tweet Pin