Question Number 40523 by scientist last updated on 23/Jul/18

$${If}\:\left(\mathrm{1}+{ax}+{bx}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{x}\right)^{\mathrm{18}} \:\:{can}\:{be}\:{expanded}\:{using} \\ $$$${binomial}\:{theorem}\:{in}\:{ascending}\:{power}\:{of}\:{x}.{Determine} \\ $$$${the}\:{value}\:{of}\:\:\:{a}\:{and}\:{b},{if}\:{the}\:{coefficient}\:{of}\:{x}^{\mathrm{3}} \:\:{and}\:{x}^{\mathrm{4}\:} \:\:{are}\:{both}\:{zero}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18
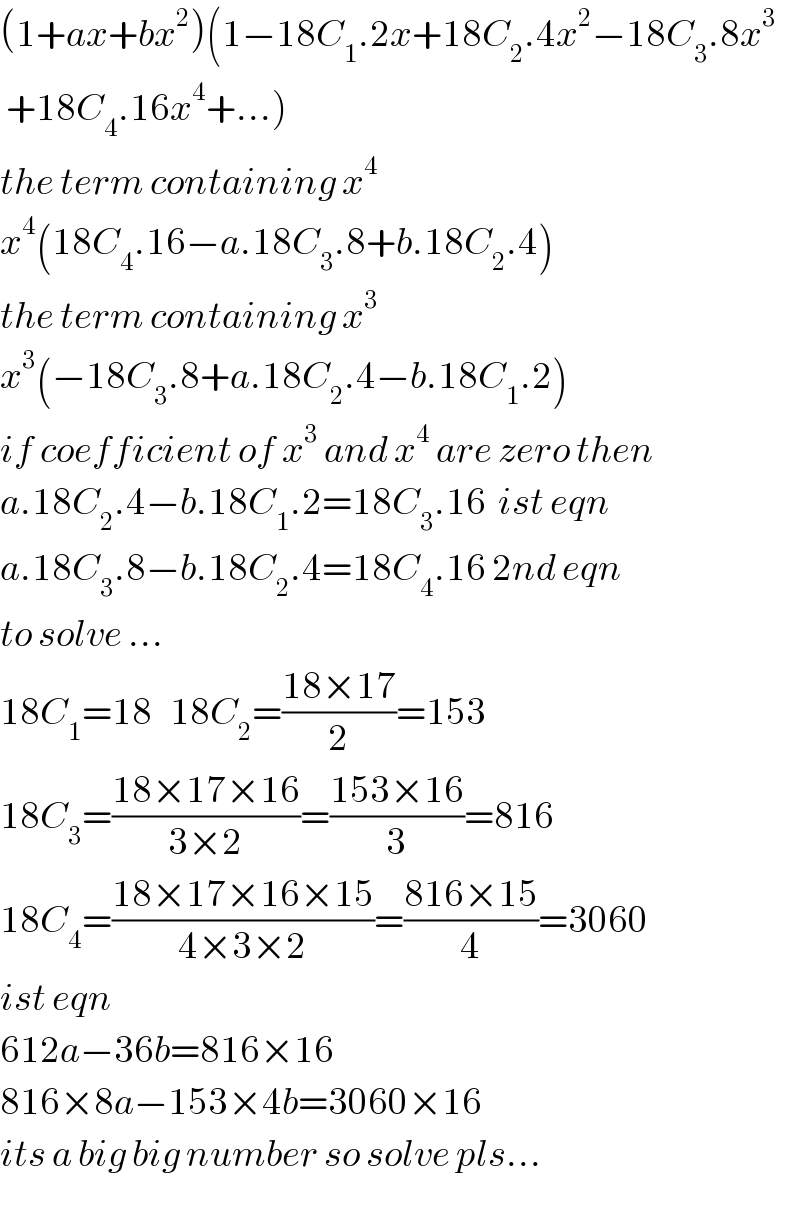
$$\left(\mathrm{1}+{ax}+{bx}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{18}{C}_{\mathrm{1}} .\mathrm{2}{x}+\mathrm{18}{C}_{\mathrm{2}} .\mathrm{4}{x}^{\mathrm{2}} −\mathrm{18}{C}_{\mathrm{3}} .\mathrm{8}{x}^{\mathrm{3}} \right. \\ $$$$\left.\:+\mathrm{18}{C}_{\mathrm{4}} .\mathrm{16}{x}^{\mathrm{4}} +…\right) \\ $$$${the}\:{term}\:{containing}\:{x}^{\mathrm{4}} \:\: \\ $$$${x}^{\mathrm{4}} \left(\mathrm{18}{C}_{\mathrm{4}} .\mathrm{16}−{a}.\mathrm{18}{C}_{\mathrm{3}} .\mathrm{8}+{b}.\mathrm{18}{C}_{\mathrm{2}} .\mathrm{4}\right) \\ $$$${the}\:{term}\:{containing}\:{x}^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} \left(−\mathrm{18}{C}_{\mathrm{3}} .\mathrm{8}+{a}.\mathrm{18}{C}_{\mathrm{2}} .\mathrm{4}−{b}.\mathrm{18}{C}_{\mathrm{1}} .\mathrm{2}\right) \\ $$$${if}\:{coefficient}\:{of}\:{x}^{\mathrm{3}} \:{and}\:{x}^{\mathrm{4}} \:{are}\:{zero}\:{then} \\ $$$${a}.\mathrm{18}{C}_{\mathrm{2}} .\mathrm{4}−{b}.\mathrm{18}{C}_{\mathrm{1}} .\mathrm{2}=\mathrm{18}{C}_{\mathrm{3}} .\mathrm{16}\:\:{ist}\:{eqn} \\ $$$${a}.\mathrm{18}{C}_{\mathrm{3}} .\mathrm{8}−{b}.\mathrm{18}{C}_{\mathrm{2}} .\mathrm{4}=\mathrm{18}{C}_{\mathrm{4}} .\mathrm{16}\:\mathrm{2}{nd}\:{eqn} \\ $$$${to}\:{solve}\:… \\ $$$$\mathrm{18}{C}_{\mathrm{1}} =\mathrm{18}\:\:\:\mathrm{18}{C}_{\mathrm{2}} =\frac{\mathrm{18}×\mathrm{17}}{\mathrm{2}}=\mathrm{153} \\ $$$$\mathrm{18}{C}_{\mathrm{3}} =\frac{\mathrm{18}×\mathrm{17}×\mathrm{16}}{\mathrm{3}×\mathrm{2}}=\frac{\mathrm{153}×\mathrm{16}}{\mathrm{3}}=\mathrm{816} \\ $$$$\mathrm{18}{C}_{\mathrm{4}} =\frac{\mathrm{18}×\mathrm{17}×\mathrm{16}×\mathrm{15}}{\mathrm{4}×\mathrm{3}×\mathrm{2}}=\frac{\mathrm{816}×\mathrm{15}}{\mathrm{4}}=\mathrm{3060} \\ $$$${ist}\:{eqn} \\ $$$$\mathrm{612}{a}−\mathrm{36}{b}=\mathrm{816}×\mathrm{16} \\ $$$$\mathrm{816}×\mathrm{8}{a}−\mathrm{153}×\mathrm{4}{b}=\mathrm{3060}×\mathrm{16} \\ $$$${its}\:{a}\:{big}\:{big}\:{number}\:{so}\:{solve}\:{pls}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18
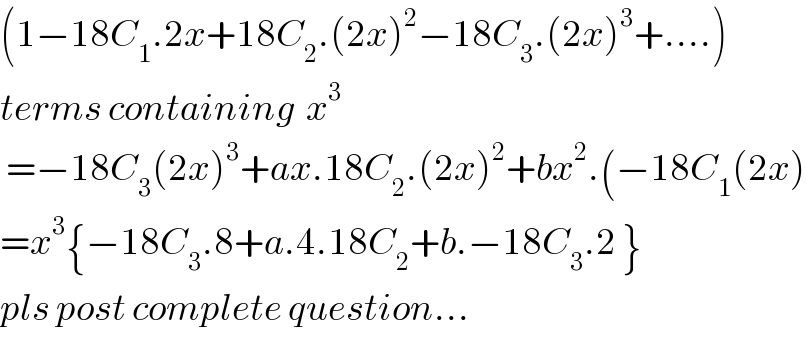
$$\left(\mathrm{1}−\mathrm{18}{C}_{\mathrm{1}} .\mathrm{2}{x}+\mathrm{18}{C}_{\mathrm{2}} .\left(\mathrm{2}{x}\right)^{\mathrm{2}} −\mathrm{18}{C}_{\mathrm{3}} .\left(\mathrm{2}{x}\right)^{\mathrm{3}} +….\right) \\ $$$${terms}\:{containing}\:\:{x}^{\mathrm{3}} \\ $$$$\:=−\mathrm{18}{C}_{\mathrm{3}} \left(\mathrm{2}{x}\right)^{\mathrm{3}} +{ax}.\mathrm{18}{C}_{\mathrm{2}} .\left(\mathrm{2}{x}\right)^{\mathrm{2}} +{bx}^{\mathrm{2}} .\left(−\mathrm{18}{C}_{\mathrm{1}} \left(\mathrm{2}{x}\right)\right. \\ $$$$={x}^{\mathrm{3}} \left\{−\mathrm{18}{C}_{\mathrm{3}} .\mathrm{8}+{a}.\mathrm{4}.\mathrm{18}{C}_{\mathrm{2}} +{b}.−\mathrm{18}{C}_{\mathrm{3}} .\mathrm{2}\:\right\} \\ $$$${pls}\:{post}\:{complete}\:{question}… \\ $$
Commented by MJS last updated on 23/Jul/18

$$\mathrm{also}\:\mathrm{the}\:\mathrm{constant}\:\mathrm{factor}\:\mathrm{of}\:{x}^{\mathrm{4}} \:\mathrm{is}\:\mathrm{zero},\:\mathrm{so}\:\mathrm{just} \\ $$$$\mathrm{continue}! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jul/18

$${ok}\:{sir}… \\ $$
