Question Number 127169 by bramlexs22 last updated on 27/Dec/20
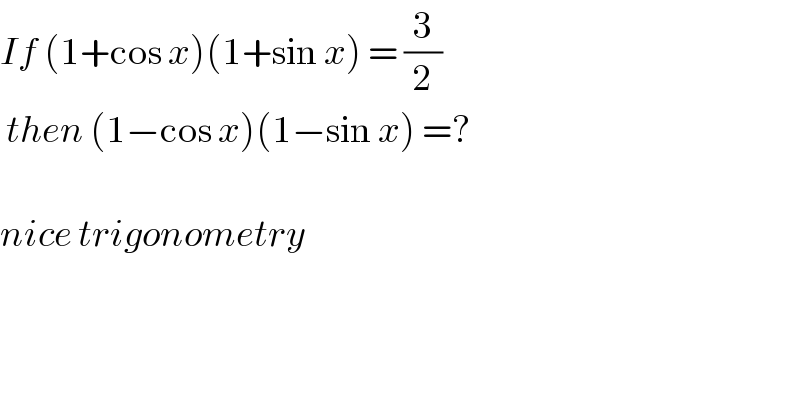
$${If}\:\left(\mathrm{1}+\mathrm{cos}\:{x}\right)\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\:=\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:{then}\:\left(\mathrm{1}−\mathrm{cos}\:{x}\right)\left(\mathrm{1}−\mathrm{sin}\:{x}\right)\:=? \\ $$$$ \\ $$$${nice}\:{trigonometry}\: \\ $$
Commented by Dwaipayan Shikari last updated on 27/Dec/20
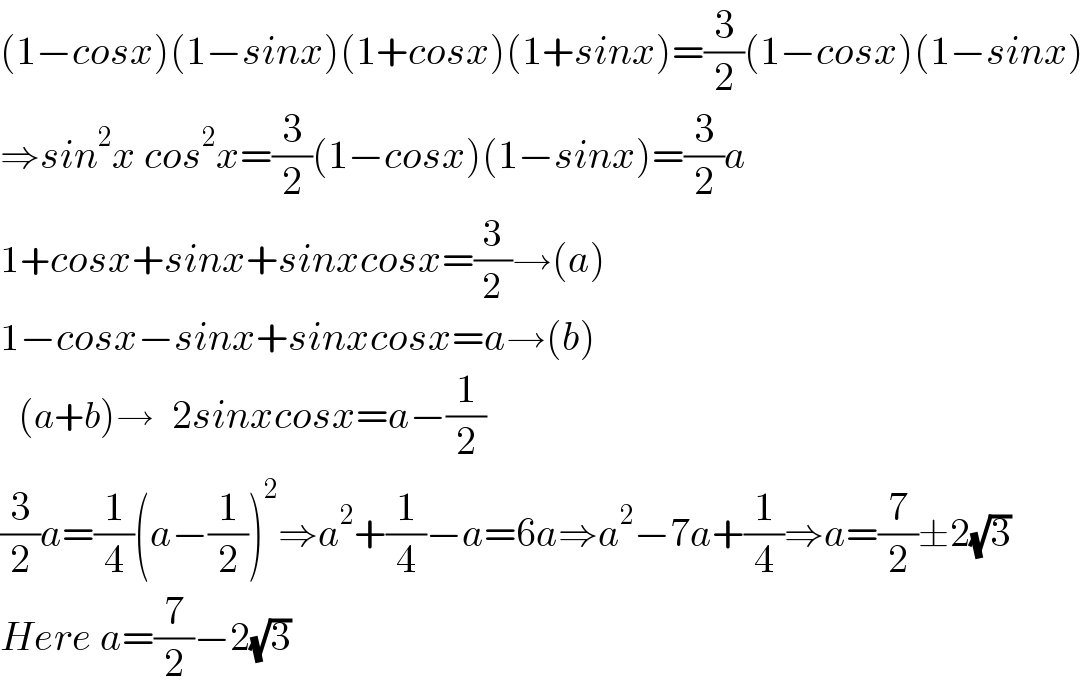
$$\left(\mathrm{1}−{cosx}\right)\left(\mathrm{1}−{sinx}\right)\left(\mathrm{1}+{cosx}\right)\left(\mathrm{1}+{sinx}\right)=\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}−{cosx}\right)\left(\mathrm{1}−{sinx}\right) \\ $$$$\Rightarrow{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}} {x}=\frac{\mathrm{3}}{\mathrm{2}}\left(\mathrm{1}−{cosx}\right)\left(\mathrm{1}−{sinx}\right)=\frac{\mathrm{3}}{\mathrm{2}}{a} \\ $$$$\mathrm{1}+{cosx}+{sinx}+{sinxcosx}=\frac{\mathrm{3}}{\mathrm{2}}\rightarrow\left({a}\right) \\ $$$$\mathrm{1}−{cosx}−{sinx}+{sinxcosx}={a}\rightarrow\left({b}\right) \\ $$$$\:\:\:\left({a}+{b}\right)\rightarrow\:\:\:\mathrm{2}{sinxcosx}={a}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{a}=\frac{\mathrm{1}}{\mathrm{4}}\left({a}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \Rightarrow{a}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}−{a}=\mathrm{6}{a}\Rightarrow{a}^{\mathrm{2}} −\mathrm{7}{a}+\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow{a}=\frac{\mathrm{7}}{\mathrm{2}}\pm\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${Here}\:{a}=\frac{\mathrm{7}}{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$
Commented by bramlexs22 last updated on 27/Dec/20

Commented by liberty last updated on 27/Dec/20
![(1+sin x)(1+cos x)=(3/2) (sin (x/2)+cos (x/2))^2 (2cos^2 (x/2))=(3/2) (sin (x/2)+cos (x/2)).cos (x/2) =± ((√3)/2) sin (x/2).cos (x/2)+cos^2 (x/2) =±((√3)/2) ((sin x)/2)+((1+cos x)/2)= ±((√3)/2) ⇒sin x+cos x = (√3)−1 ; other value is outside the range . note: range of (sin x+cos x)= [−(√2) ,(√2) ] and−1−(√3) <−(√2) ∴ (sin x+cos x)^2 =((√3)−1)^2 1+2sin xcos x = 4−2(√3) then f(x)=(1−sin x)(1−cos x) = 1−(sin x+cos x)+sin xcos x = 1−((√3)−1)+((3−2(√3))/2) = ((7−4(√3))/2) ≈ 0.035898](https://www.tinkutara.com/question/Q127193.png)
$$\left(\mathrm{1}+\mathrm{sin}\:{x}\right)\left(\mathrm{1}+\mathrm{cos}\:{x}\right)=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left(\mathrm{sin}\:\frac{{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{2cos}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left(\mathrm{sin}\:\frac{{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\right).\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\:=\pm\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\frac{{x}}{\mathrm{2}}.\mathrm{cos}\:\frac{{x}}{\mathrm{2}}+\mathrm{cos}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\:=\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\frac{\mathrm{sin}\:{x}}{\mathrm{2}}+\frac{\mathrm{1}+\mathrm{cos}\:{x}}{\mathrm{2}}=\:\pm\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\:=\:\sqrt{\mathrm{3}}−\mathrm{1}\:;\:{other}\:{value}\:{is} \\ $$$${outside}\:{the}\:{range}\:. \\ $$$${note}:\:{range}\:{of}\:\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)=\:\left[−\sqrt{\mathrm{2}}\:,\sqrt{\mathrm{2}}\:\right]\: \\ $$$${and}−\mathrm{1}−\sqrt{\mathrm{3}}\:<−\sqrt{\mathrm{2}}\: \\ $$$$\therefore\:\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)^{\mathrm{2}} =\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\mathrm{1}+\mathrm{2sin}\:{x}\mathrm{cos}\:{x}\:=\:\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${then}\:{f}\left({x}\right)=\left(\mathrm{1}−\mathrm{sin}\:{x}\right)\left(\mathrm{1}−\mathrm{cos}\:{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}−\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)+\mathrm{sin}\:{x}\mathrm{cos}\:{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{1}−\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)+\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\approx\:\mathrm{0}.\mathrm{035898} \\ $$$$ \\ $$
