Menu Close

If-1-lo-g-2-x-1-3-1-log-2-x-1-3-1-0-x-

Tinku Tara 0 Comments
Pin




Question Number 186419 by mnjuly1970 last updated on 04/Feb/23
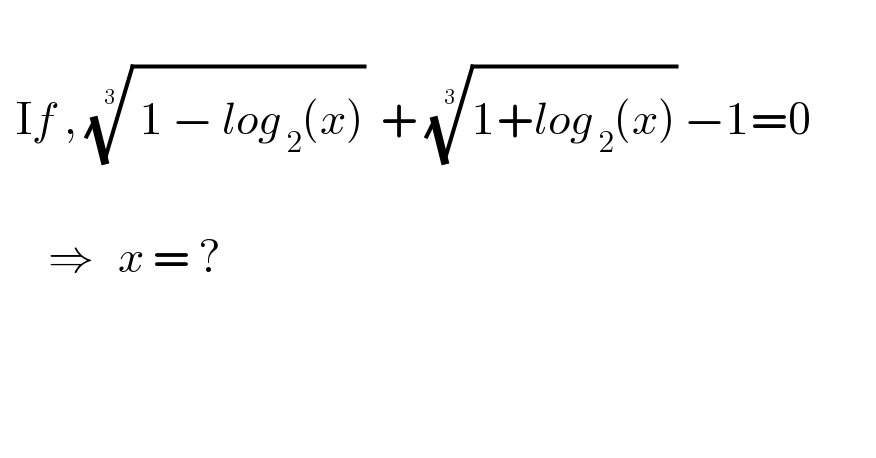
If , (( 1 − lo^ g_( 2) (x)))^(1/3) + ((1+^ log_( 2) (x)))^(1/3) −1=0 ⇒ x = ?
$$ \\ $$$$\:\:\mathrm{I}{f}\:,\:\sqrt[{\mathrm{3}}]{\:\mathrm{1}\:−\:{l}\overset{} {{o}g}_{\:\mathrm{2}} \left({x}\right)}\:\:+\:\sqrt[{\mathrm{3}}]{\mathrm{1}\overset{} {+}{log}_{\:\mathrm{2}} \left({x}\right)}\:−\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\Rightarrow\:\:\:{x}\:=\:?\:\:\:\: \\ $$
Answered by cortano1 last updated on 04/Feb/23
We know that if a+b+c = 0 then a^3 +b^3 +c^3 = 3abc ⇒((1−log _2 x))^(1/3) +((1+log _2 x))^(1/3) +(−1)=0 ⇒(1−log _2 x)+(1+log _2 x)+(−1)=−3(((1−(log _2 x)^2 ))^(1/3) ⇒−(1/3) = ((1−(log _2 x)^2 ))^(1/3) ⇒(log _2 x)^2 = ((28)/(27)) ⇒ { ((x=2^(√((28)/(27))) =2^((2(√7))/(3(√3))) )),((x= (1/((2^((2(√7))/( 3(√3))) ))))) :}
$$\:{We}\:{know}\:{that}\:{if}\:{a}+{b}+{c}\:=\:\mathrm{0}\: \\ $$$$\:{then}\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \:=\:\mathrm{3}{abc}\: \\ $$$$\Rightarrow\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{log}\:_{\mathrm{2}} {x}}\:+\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{log}\:_{\mathrm{2}} {x}}+\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{1}−\mathrm{log}\:_{\mathrm{2}} {x}\right)+\left(\mathrm{1}+\mathrm{log}\:_{\mathrm{2}} {x}\right)+\left(−\mathrm{1}\right)=−\mathrm{3}\sqrt[{\mathrm{3}}]{\left(\mathrm{1}−\left(\mathrm{log}\:_{\mathrm{2}} {x}\right)^{\mathrm{2}} \right.} \\ $$$$\Rightarrow−\frac{\mathrm{1}}{\mathrm{3}}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{1}−\left(\mathrm{log}\:_{\mathrm{2}} {x}\right)^{\mathrm{2}} }\: \\ $$$$\Rightarrow\left(\mathrm{log}\:_{\mathrm{2}} {x}\right)^{\mathrm{2}} =\:\frac{\mathrm{28}}{\mathrm{27}} \\ $$$$\Rightarrow\begin{cases}{{x}=\mathrm{2}^{\sqrt{\frac{\mathrm{28}}{\mathrm{27}}}} =\mathrm{2}^{\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\mathrm{3}\sqrt{\mathrm{3}}}} }\\{{x}=\:\frac{\mathrm{1}}{\left(\mathrm{2}^{\frac{\mathrm{2}\sqrt{\mathrm{7}}}{\:\mathrm{3}\sqrt{\mathrm{3}}}} \right)}}\end{cases} \\ $$
Commented by mnjuly1970 last updated on 04/Feb/23
thanks alot sir cortsno
$${thanks}\:{alot}\:\:{sir}\:{cortsno} \\ $$
Answered by mahdipoor last updated on 04/Feb/23
x=2^(y^3 −1) ⇒^3 (√(2−y^3 ))+y−1=0⇒ (^3 (√(2−y^3 )))^3 =(1−y)^3 ⇒2−y^3 =1−3y+3y^2 −y^3 ⇒3y^2 −3y−1=0⇒y=((3±(√(21)))/6)=(1/2)±((√(21))/6) y^3 −1=(1/8)±((√(21))/8)+((21)/(24))±((7(√(21)))/(72))−1=±(2/9)(√(21)) ⇒x=2^∧ (±((2(√(21)))/9))
$${x}=\mathrm{2}^{{y}^{\mathrm{3}} −\mathrm{1}} \Rightarrow^{\mathrm{3}} \sqrt{\mathrm{2}−{y}^{\mathrm{3}} }+{y}−\mathrm{1}=\mathrm{0}\Rightarrow \\ $$$$\left(^{\mathrm{3}} \sqrt{\mathrm{2}−{y}^{\mathrm{3}} }\right)^{\mathrm{3}} =\left(\mathrm{1}−{y}\right)^{\mathrm{3}} \Rightarrow\mathrm{2}−{y}^{\mathrm{3}} =\mathrm{1}−\mathrm{3}{y}+\mathrm{3}{y}^{\mathrm{2}} −{y}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{3}{y}^{\mathrm{2}} −\mathrm{3}{y}−\mathrm{1}=\mathrm{0}\Rightarrow{y}=\frac{\mathrm{3}\pm\sqrt{\mathrm{21}}}{\mathrm{6}}=\frac{\mathrm{1}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{21}}}{\mathrm{6}} \\ $$$${y}^{\mathrm{3}} −\mathrm{1}=\frac{\mathrm{1}}{\mathrm{8}}\pm\frac{\sqrt{\mathrm{21}}}{\mathrm{8}}+\frac{\mathrm{21}}{\mathrm{24}}\pm\frac{\mathrm{7}\sqrt{\mathrm{21}}}{\mathrm{72}}−\mathrm{1}=\pm\frac{\mathrm{2}}{\mathrm{9}}\sqrt{\mathrm{21}} \\ $$$$\Rightarrow{x}=\mathrm{2}^{\wedge} \left(\pm\frac{\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{9}}\right) \\ $$
Commented by mnjuly1970 last updated on 04/Feb/23
manoon ostad ali bood
$${manoon}\:{ostad}\:{ali}\:{bood} \\ $$
Answered by Rasheed.Sindhi last updated on 04/Feb/23
((1−log_2 x ))^(1/3) +((1+log_2 x ))^(1/3) −1=0 (((1−log_2 x ))^(1/3) +((1+log_2 x ))^(1/3) )^3 =1 1−log_2 x+1+log_2 x+3(1−log_2 x)(1+log_2 x)(((1−log_2 x ))^(1/3) +((1+log_2 x ))^(1/3) )=1 2+3(((1−log_2 x))^(1/3) )(((1+log_2 x))^(1/3) )(1)=1 2+3(((1−(log_2 x )^2 ))^(1/3) )=1 ((1−(log_2 x )^2 ))^(1/3) =−1/3 1−(log_2 x )^2 =−(1/(27)) (log_2 x )^2 =1+(1/(27))=((28)/(27)) log_2 x =((±2(√7) )/(3(√3)))∙((±2(√(21)))/9) x=2^((±2(√(21)))/9)
$$\:\:\:\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{log}_{\mathrm{2}} {x}\:}\:+\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{log}_{\mathrm{2}} {x}\:}\:−\mathrm{1}=\mathrm{0}\:\:\:\:\:\:\: \\ $$$$\left(\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{log}_{\mathrm{2}} {x}\:}\:+\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{log}_{\mathrm{2}} {x}\:}\:\right)^{\mathrm{3}} =\mathrm{1} \\ $$$$\mathrm{1}−\cancel{\mathrm{log}_{\mathrm{2}} {x}}+\mathrm{1}+\cancel{\mathrm{log}_{\mathrm{2}} {x}}+\mathrm{3}\left(\mathrm{1}−\mathrm{log}_{\mathrm{2}} {x}\right)\left(\mathrm{1}+\mathrm{log}_{\mathrm{2}} {x}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{log}_{\mathrm{2}} {x}\:}\:+\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{log}_{\mathrm{2}} {x}\:}\:\right)=\mathrm{1} \\ $$$$\mathrm{2}+\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\mathrm{1}−\mathrm{log}_{\mathrm{2}} {x}}\right)\left(\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{log}_{\mathrm{2}} {x}}\right)\left(\mathrm{1}\right)=\mathrm{1} \\ $$$$\mathrm{2}+\mathrm{3}\left(\sqrt[{\mathrm{3}}]{\mathrm{1}−\left(\mathrm{log}_{\mathrm{2}} {x}\:\right)^{\mathrm{2}} }\right)=\mathrm{1} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{1}−\left(\mathrm{log}_{\mathrm{2}} {x}\:\right)^{\mathrm{2}} }=−\mathrm{1}/\mathrm{3} \\ $$$$\:\:\:\:\mathrm{1}−\left(\mathrm{log}_{\mathrm{2}} {x}\:\right)^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{27}} \\ $$$$\left(\mathrm{log}_{\mathrm{2}} {x}\:\right)^{\mathrm{2}} =\mathrm{1}+\frac{\mathrm{1}}{\mathrm{27}}=\frac{\mathrm{28}}{\mathrm{27}} \\ $$$$\mathrm{log}_{\mathrm{2}} {x}\:=\frac{\pm\mathrm{2}\sqrt{\mathrm{7}}\:}{\mathrm{3}\sqrt{\mathrm{3}}}\centerdot\frac{\pm\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{9}} \\ $$$$\:\:\:\:{x}=\mathrm{2}^{\frac{\pm\mathrm{2}\sqrt{\mathrm{21}}}{\mathrm{9}}} \\ $$
Commented by mnjuly1970 last updated on 04/Feb/23
thank you so much sir rasheed
$${thank}\:{you}\:{so}\:{much} \\ $$$${sir}\:{rasheed} \\ $$
Commented by mahdipoor last updated on 04/Feb/23
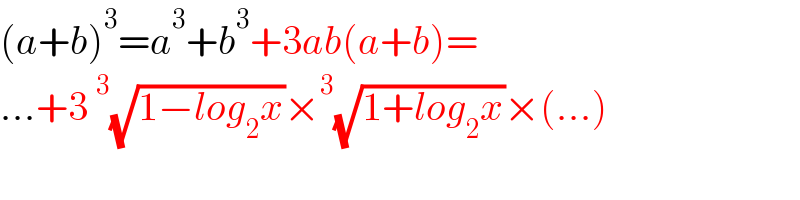
(a+b)^3 =a^3 +b^3 +3ab(a+b)= ...+3^3 (√(1−log_2 x))×^3 (√(1+log_2 x))×(...)
$$\left({a}+{b}\right)^{\mathrm{3}} ={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +\mathrm{3}{ab}\left({a}+{b}\right)= \\ $$$$…+\mathrm{3}\:^{\mathrm{3}} \sqrt{\mathrm{1}−{log}_{\mathrm{2}} {x}}×^{\mathrm{3}} \sqrt{\mathrm{1}+{log}_{\mathrm{2}} {x}}×\left(…\right) \\ $$$$ \\ $$
Commented by Rasheed.Sindhi last updated on 04/Feb/23
Thank you sir,I′ve corrected.
$$\mathcal{T}{hank}\:{you}\:{sir},{I}'{ve}\:{corrected}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *