Question Number 147932 by mathdanisur last updated on 24/Jul/21
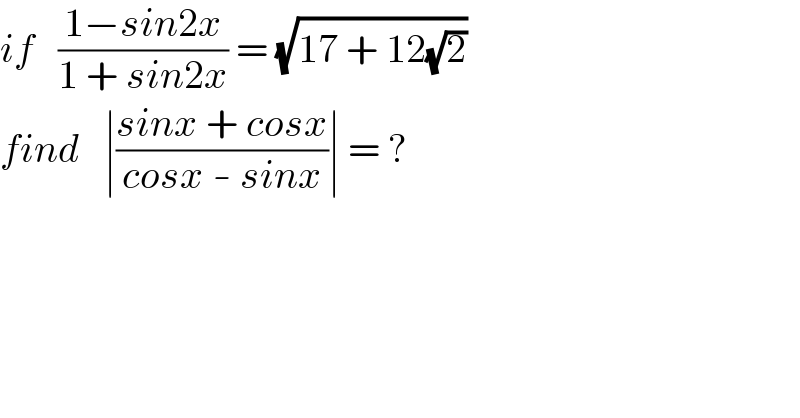
$${if}\:\:\:\frac{\mathrm{1}−{sin}\mathrm{2}{x}}{\mathrm{1}\:+\:{sin}\mathrm{2}{x}}\:=\:\sqrt{\mathrm{17}\:+\:\mathrm{12}\sqrt{\mathrm{2}}} \\ $$$${find}\:\:\:\mid\frac{{sinx}\:+\:{cosx}}{{cosx}\:-\:{sinx}}\mid\:=\:? \\ $$
Answered by iloveisrael last updated on 24/Jul/21
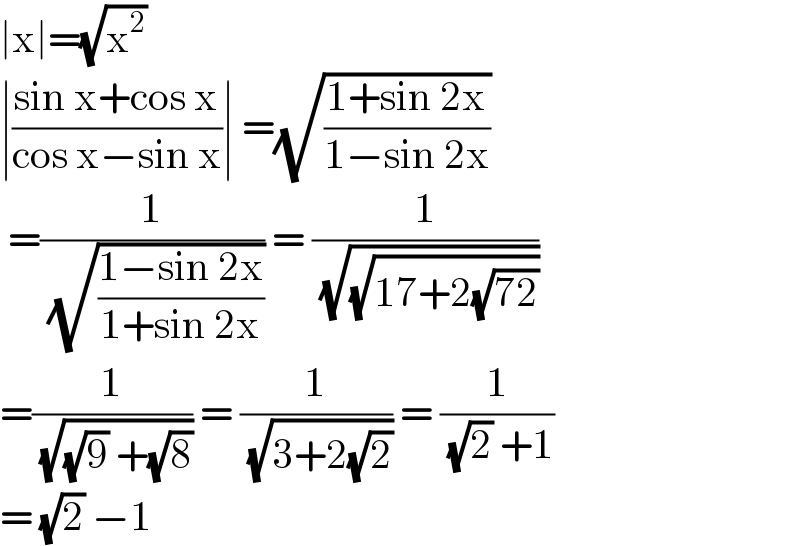
$$\mid\mathrm{x}\mid=\sqrt{\mathrm{x}^{\mathrm{2}} } \\ $$$$\mid\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}\mid\:=\sqrt{\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{2x}}{\mathrm{1}−\mathrm{sin}\:\mathrm{2x}}}\: \\ $$$$\:=\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}−\mathrm{sin}\:\mathrm{2x}}{\mathrm{1}+\mathrm{sin}\:\mathrm{2x}}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\sqrt{\mathrm{17}+\mathrm{2}\sqrt{\mathrm{72}}}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\sqrt{\mathrm{9}}\:+\sqrt{\mathrm{8}}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:+\mathrm{1}} \\ $$$$=\:\sqrt{\mathrm{2}}\:−\mathrm{1}\: \\ $$
Commented by mathdanisur last updated on 24/Jul/21

$${Thank}\:{you}\:{Ser} \\ $$
