Menu Close

If-1-sinx-sin-2-x-sin-3-x-4-2-3-x-

Tinku Tara 0 Comments
Pin




Question Number 175904 by BaliramKumar last updated on 09/Sep/22
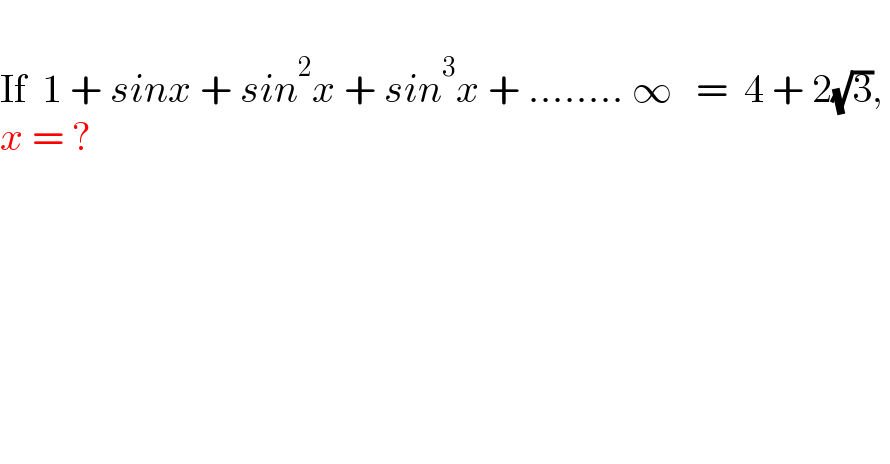
If 1 + sinx + sin^2 x + sin^3 x + ........ ∞ = 4 + 2(√3), x = ?
$$ \\ $$$$\mathrm{If}\:\:\mathrm{1}\:+\:{sinx}\:+\:{sin}^{\mathrm{2}} {x}\:+\:{sin}^{\mathrm{3}} {x}\:+\:……..\:\infty\:\:\:=\:\:\mathrm{4}\:+\:\mathrm{2}\sqrt{\mathrm{3}},\: \\ $$$${x}\:=\:? \\ $$
Commented by infinityaction last updated on 09/Sep/22
g.p. sum (1/(1−sinx )) = 4+2(√3) 1−sinx = (1/(4+2(√3))) = ((4−2(√3))/(16−12)) 1−sinx = ((4−2(√3))/4) = 1−((√3)/2) sinx = ((√3)/2) x = 60°
$${g}.{p}.\:{sum} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}{x}\:}\:=\:\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\mathrm{1}−\mathrm{sin}{x}\:=\:\frac{\mathrm{1}}{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}\:=\:\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{16}−\mathrm{12}} \\ $$$$\mathrm{1}−\mathrm{sin}{x}\:\:=\:\:\frac{\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}}\:=\:\mathrm{1}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\:\mathrm{sin}{x}\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\: \\ $$$$\:\:\:{x}\:=\:\:\mathrm{60}° \\ $$
Answered by Rasheed.Sindhi last updated on 09/Sep/22
AnOther way... Let S=1 + sinx + sin^2 x + sin^3 x + ........ ∞...(i) sinx∙S =sinx + sin^2 x + sin^3 x + ........ ∞...(ii) (i)−(ii): S(1−sinx)=1 S=(1/(1−sinx ))=4 + 2(√3) 1−sinx=(1/(4 + 2(√3))) sinx=1−(1/(4 + 2(√3)))=((3 + 2(√3) )/(4+2(√3)))∙((4 − 2(√3))/(4 − 2(√3))) =((12−6(√3) +8(√3) −12)/(16−12)) =((2(√3) )/4)=((√3)/2) x=60°
$$\mathrm{AnOther}\:\mathrm{way}… \\ $$$$\mathrm{L}{et}\:{S}=\mathrm{1}\:+\:{sinx}\:+\:{sin}^{\mathrm{2}} {x}\:+\:{sin}^{\mathrm{3}} {x}\:+\:……..\:\infty…\left({i}\right) \\ $$$$\mathrm{sin}{x}\centerdot{S}\:={sinx}\:+\:{sin}^{\mathrm{2}} {x}\:+\:{sin}^{\mathrm{3}} {x}\:+\:……..\:\infty…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${S}\left(\mathrm{1}−\mathrm{sin}{x}\right)=\mathrm{1} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{sin}{x}\:}=\mathrm{4}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{1}−\mathrm{sin}{x}=\frac{\mathrm{1}}{\mathrm{4}\:+\:\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{sin}{x}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}\:+\:\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\mathrm{3}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\:}{\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}\centerdot\frac{\mathrm{4}\:−\:\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}\:−\:\mathrm{2}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{12}−\mathrm{6}\sqrt{\mathrm{3}}\:+\mathrm{8}\sqrt{\mathrm{3}}\:−\mathrm{12}}{\mathrm{16}−\mathrm{12}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}\sqrt{\mathrm{3}}\:}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}=\mathrm{60}° \\ $$
Answered by Rasheed.Sindhi last updated on 09/Sep/22
≪AnOther Approach...≫ 1 + sinx + sin^2 x + sin^3 x + ........ ∞ = 4 + 2(√3), x=? Let S=1 + sinx + sin^2 x + sin^3 x + ........ ∞ S=1+sinx(1 + sinx + sin^2 x + sin^3 x + ........ ∞ S=1+sinx.S S−sinx.S=1 S=(1/(1−sinx))= 4 + 2(√3) 1−sinx=(1/( 4 + 2(√3) ))∙((4 − 2(√3) )/(4 − 2(√3) )) sinx=1−((4 − 2(√3) )/(16−12))=((4−4+2(√3))/4) sinx=(((√3) )/2) x=60°
$$\:\:\:\:\:\:\ll\mathrm{AnOther}\:\mathrm{Approach}…\gg \\ $$$$\mathrm{1}\:+\:{sinx}\:+\:{sin}^{\mathrm{2}} {x}\:+\:{sin}^{\mathrm{3}} {x}\:+\:……..\:\infty\:\:\:=\:\:\mathrm{4}\:+\:\mathrm{2}\sqrt{\mathrm{3}},\:{x}=? \\ $$$${Let}\:{S}=\mathrm{1}\:+\:{sinx}\:+\:{sin}^{\mathrm{2}} {x}\:+\:{sin}^{\mathrm{3}} {x}\:+\:……..\:\infty \\ $$$${S}=\mathrm{1}+{sinx}\left(\mathrm{1}\:+\:{sinx}\:+\:{sin}^{\mathrm{2}} {x}\:+\:{sin}^{\mathrm{3}} {x}\:+\:……..\:\infty\right. \\ $$$${S}=\mathrm{1}+{sinx}.{S} \\ $$$${S}−{sinx}.{S}=\mathrm{1} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{1}−{sinx}}=\:\mathrm{4}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$$$\:\:\:\:\:\mathrm{1}−{sinx}=\frac{\mathrm{1}}{\:\mathrm{4}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\:}\centerdot\frac{\mathrm{4}\:−\:\mathrm{2}\sqrt{\mathrm{3}}\:}{\mathrm{4}\:−\:\mathrm{2}\sqrt{\mathrm{3}}\:} \\ $$$$\:\:\:\:\:\:{sinx}=\mathrm{1}−\frac{\mathrm{4}\:−\:\mathrm{2}\sqrt{\mathrm{3}}\:}{\mathrm{16}−\mathrm{12}}=\frac{\mathrm{4}−\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:{sinx}=\frac{\sqrt{\mathrm{3}}\:}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:{x}=\mathrm{60}° \\ $$
Commented by peter frank last updated on 09/Sep/22
thanks
$$\mathrm{thanks} \\ $$
Commented by Tawa11 last updated on 15/Sep/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *