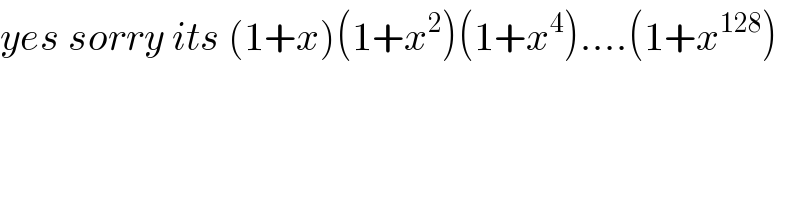Question Number 96318 by M±th+et+s last updated on 31/May/20
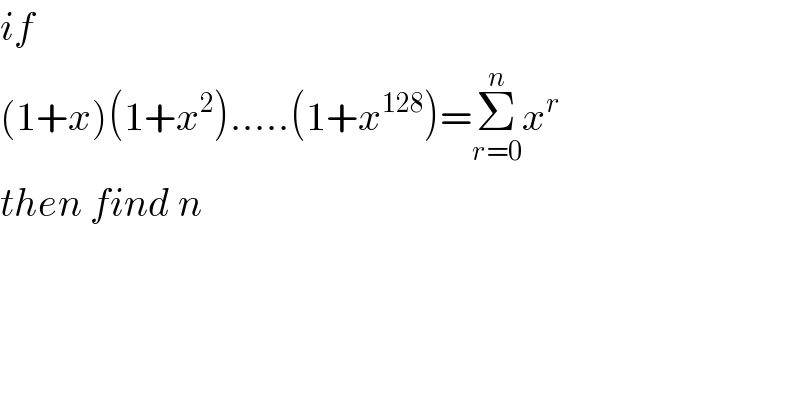
Commented by mr W last updated on 31/May/20
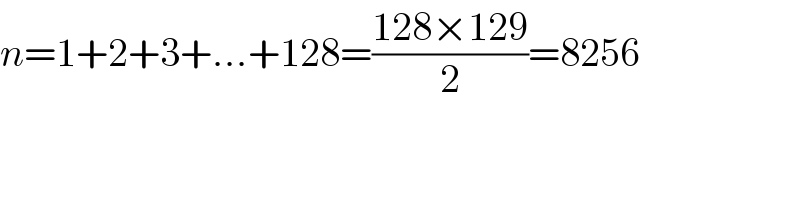
Commented by M±th+et+s last updated on 31/May/20

Commented by mr W last updated on 31/May/20
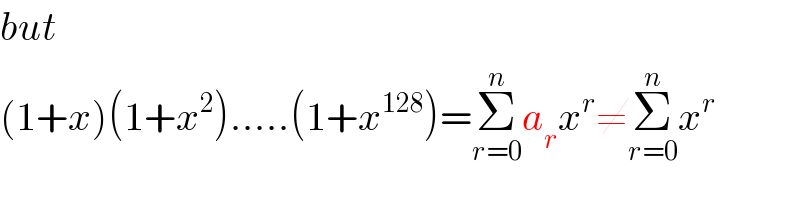
Commented by M±th+et+s last updated on 31/May/20