Question Number 165545 by HongKing last updated on 03/Feb/22
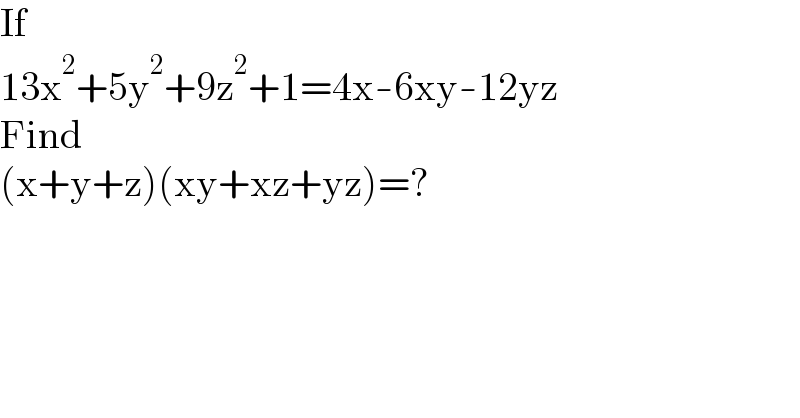
$$\mathrm{If} \\ $$$$\mathrm{13x}^{\mathrm{2}} +\mathrm{5y}^{\mathrm{2}} +\mathrm{9z}^{\mathrm{2}} +\mathrm{1}=\mathrm{4x}-\mathrm{6xy}-\mathrm{12yz} \\ $$$$\mathrm{Find} \\ $$$$\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\left(\mathrm{xy}+\mathrm{xz}+\mathrm{yz}\right)=? \\ $$
Commented by MJS_new last updated on 04/Feb/22

$$\mathrm{if}\:{x},\:{y},\:{z}\:\in\mathbb{C}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{unique}:\:\mathrm{we}\:\mathrm{can}\:\mathrm{choose} \\ $$$$\mathrm{two}\:\mathrm{variables}\:\mathrm{and}\:\mathrm{solve}\:\mathrm{for}\:\mathrm{the}\:\mathrm{third}\:\mathrm{one}. \\ $$
Commented by som(math1967) last updated on 04/Feb/22

$${yes}\:{sir} \\ $$
Commented by HongKing last updated on 06/Feb/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
Answered by som(math1967) last updated on 03/Feb/22
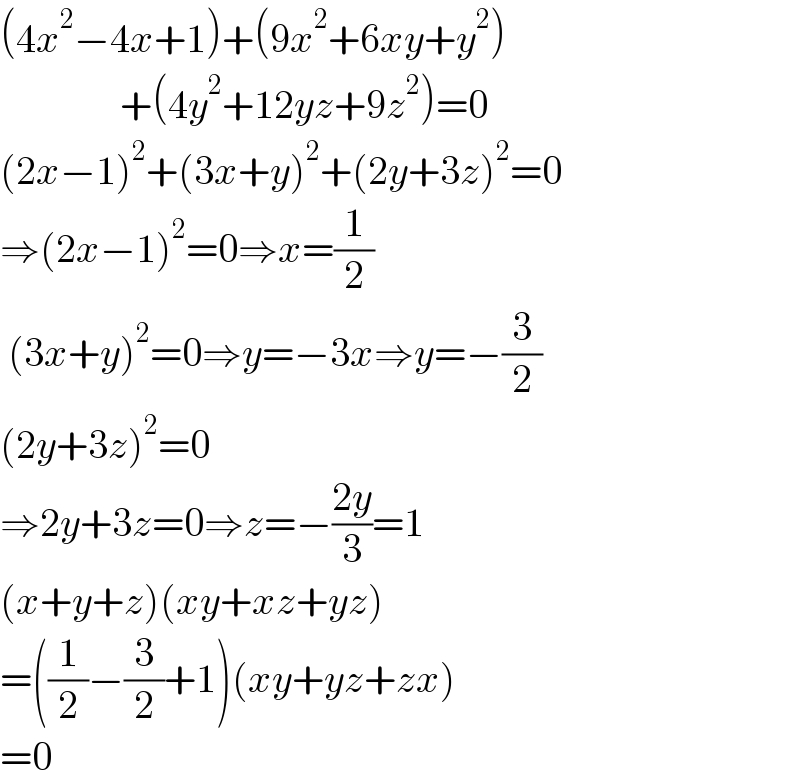
$$\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}\right)+\left(\mathrm{9}{x}^{\mathrm{2}} +\mathrm{6}{xy}+{y}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\mathrm{4}{y}^{\mathrm{2}} +\mathrm{12}{yz}+\mathrm{9}{z}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{3}{x}+{y}\right)^{\mathrm{2}} +\left(\mathrm{2}{y}+\mathrm{3}{z}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\left(\mathrm{3}{x}+{y}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow{y}=−\mathrm{3}{x}\Rightarrow{y}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}{y}+\mathrm{3}{z}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{y}+\mathrm{3}{z}=\mathrm{0}\Rightarrow{z}=−\frac{\mathrm{2}{y}}{\mathrm{3}}=\mathrm{1} \\ $$$$\left({x}+{y}+{z}\right)\left({xy}+{xz}+{yz}\right) \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}\right)\left({xy}+{yz}+{zx}\right) \\ $$$$=\mathrm{0} \\ $$
Commented by HongKing last updated on 06/Feb/22
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{Sir} \\ $$
